当前位置：试卷中心 > 试卷详情

2022-2023学年四川省达州市渠县中学八年级（下）期中数学试卷

发布：2024/9/7 5:0:8

1．下列图形中既是轴对称图形又是中心对称图形的是（　　）
A． B． C． D．
组卷：17引用：1难度：0.8
解析
2．已知x＞y,则下列不等式一定成立的是（　　）
A．x-3＞y-2 B．-3x+6＞-3y+6
C．ax-5＞ay-5 D．（a²+1）x＞（a²+1）y
组卷：370引用：2难度：0.8
解析
3．已知点P（a-1，-a）在平面直角坐标系的第四象限，则a的取值范围在数轴上可表示为（　　）
A． B．
C． D．
组卷：367引用：10难度：0.6
解析
4．下列因式分解正确的是（　　）
A．2a²-4a=2（a²+a） B．-a²+4=（a+2）（a-2）
C．a²-10a+25=a（a-10）+25 D．a²-2a+1=（-a+1）²
组卷：199引用：2难度：0.7
解析
5．如图，在△ABC中，∠B=41°，将△ABC绕点A逆时针旋转至△ADE处，使点B落在BC的延长线上的D点处，则∠BDE=（　　）
A．90° B．82° C．80° D．81°
组卷：241引用：9难度：0.7
解析
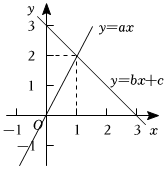6．观察图中的函数图象，则关于x的不等式（a-b）x＞c的解集为（　　）
A．x＜2 B．x＜1 C．x＞2 D．x＞1
组卷：572引用：2难度：0.7
解析
7．如果不等式bx＞a的解集是x＜3，则下列结论正确的是（　　）
A．a＞0 B．b＞0 C．a＜0 D．b＜0
组卷：201引用：1难度：0.7
解析
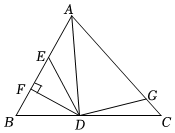8．如图，AD是△ABC的角平分线，DF⊥AB于点F，且DE=DG，S_△ADG=12，S_△AED=9，则△DEF的面积为（　　）
A．1 B．1.5 C．2 D．3
组卷：156引用：1难度：0.7
解析

24．阅读下列文字与例题，并解答：
将一个多项式分组进行因式分解后，可用提公因式法或公式法继续分解的方法称作分组分解法．例如：以下式子的分解因式的方法就称为分组分解法．a²+2ab+b²+ac+bc
原式=（a²+2ab+b²）+（ac+bc）=（a+b）²+c（a+b）=（a+b）（a+b+c）．
（1）试用“分组分解法”因式分解：x²-y²+xz-yz.
（2）已知四个实数a,b,c,d,满足a≠b,c≠d,并且a²+ac=3k,b²+bc=3k,c²+ac=6k,d²+ad=6k,同时成立，
①当k=1时，求a+c的值；
②当k≠0时，用含a的代数式分别表示b,c,d.
组卷：99引用：1难度：0.7
解析
25．【模型建立】（1）如图1，等腰Rt△ABC中，∠ACB=90°，CB=CA，直线ED经过点C，过点A作AD⊥ED于点D，过点B作BE⊥ED于点E，求证：△BEC≌△CDA．
【模型应用】（2）如图2，已知直线l₁：y=3x+6与x轴交于点A，与y轴交于点B，将直线l₁绕点A逆时针旋转45°至直线l₂，求直线l₂的函数表达式；
（3）如图3，平面直角坐标系内有一点B（5，-6），过点B作BA⊥x轴于点A、BC⊥y轴于点C，点P是直线AB上的动点，点D是直线y=-2x+2上的动点且在第四象限内．试探究△CPD能否成为等腰直角三角形？若能，求出点D的坐标，若不能，请说明理由．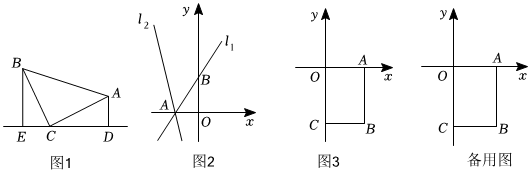
组卷：323引用：2难度：0.5
解析