2023-2024学年重庆市高二（上）入学数学试卷

一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

• 1．已知复数z=1+2i（i为虚数单位），则

  z

  的虚部为（　　）

  A．2

  B．-2

  C．2i

  D．-2i
  组卷：57引用：3难度：0.9

  解析

• 2．已知向量

  a

  =（cos120°，sin120°），

  b

  =（1，0），则

  a

  在

  b

  上的投影向量为（　　）

  A．- 3 2 b

  B．- 1 2 b

  C． 1 2 b

  D． 3 2 b
  组卷：89引用：5难度：0.7

  解析

• 3．在△ABC中，

  cos

  A

  =

  3

  5

  ，tanB=2，则tan（A+B）=（　　）

  A．2

  B． 5 3

  C．-2

  D． - 5 3
  组卷：118引用：4难度：0.7

  解析

• 4．已知α，β是空间中两个不同的平面，m,n是空间中两条不同的直线，则（　　）

  A．若m∥α，n∥α，则m∥n	B．若m∥α，m∥β，则α∥β
  C．若α⊥β，m⊂α，则m⊥β	D．若m⊥α，n⊥β，m⊥n,则α⊥β
  组卷：53引用：3难度：0.7

  解析

• 5．已知函数

  y

  =

  1

  +

  cos

  2

  ωx

  2

  （

  ω

  ＞

  0

  ）

  在

  [

  -

  π

  4

  ，

  π

  6

  ]

  上的最小值为

  1

  4

  ，则ω的值为（　　）

  A．1

  B． 2 3

  C． 4 3

  D．2
  组卷：59引用：2难度：0.7

  解析

• 6．某圆台的侧面展开是一个半圆环（如图所示），且其中内、外半圆弧所在圆的半径分别为2和6，则该圆台的体积为（　　）

  A． 14 3 3 π

  B． 26 3 3 π

  C． 26 3 π

  D． 52 3 π
  组卷：79引用：4难度：0.7

  解析

• 7．如图，在四棱锥P-ABCD中，PA⊥平面ABCD，正方形ABCD的边长为2，PA=4，E为侧棱PC的中点，则异面直线BE与PA所成角的正切值为（　　）

  A． 2 4

  B． 2

  C．1

  D． 2 2
  组卷：436引用：7难度：0.7

  解析

四、解答题：本大题共6个大题，共70分．解答应写出文字说明、证明过程或演算步骤．

• 21．函数f（x）=Msin（ωx+φ）（M＞0，ω＞0，|φ|＜

  π

  2

  ）的部分图象如图所示．已知A（-

  1

  6

  ，0），B（

  1

  3

  ，M），C（x₀，-M），AB⊥AC．
  （1）求x₀和f（x）的解析式；
  （2）将f（x）的图象向右平移

  1

  3

  个单位长度，再将得到的图象上各点的横坐标缩短为原来的

  1

  2

  ，纵坐标不变，得到函数g（x）的图象，求g（x）在[0，

  1

  2

  ]上的值域．
  组卷：155引用：4难度：0.5

  解析

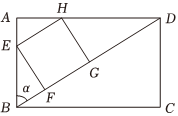• 22．中国剪纸是一种民间艺术．具有广泛的群众基础，交融于各族人民的社会生活，现有一张矩形卡片ABCD，对角线长为t（t为常数），从△ABD中裁出一个内接正方形纸片EFGH，使得点E，H分别AB，AD上，设

  ∠

  DBA

  =

  α

  （

  0

  ＜

  α

  ＜

  π

  2

  ）

  ，矩形纸片ABCD的面积为S₁，正方形纸片EFGH的面积为S₂．
  （1）当

  α

  =

  π

  3

  时，求正方形纸片EFGH的边长（结果用t表示）；
  （2）当α变化时，求

  S

  2

  S

  1

  的最大值及对应的α值．
  组卷：44引用：3难度：0.5

  解析