当前位置：试卷中心 > 试卷详情

2022-2023学年浙江省杭州四中吴山校区高二（上）期中数学试卷

发布：2024/7/14 8:0:9

1．直线
y
=
-
2
x
+
3
的斜率是（　　）
A．2 B．
1
2
C．
-
1
2
D．-2
组卷：20引用：2难度：0.8
解析
2．圆心为（-1，2），半径r=3的圆的标准方程为（　　）
A．（x-1）²+（y+2）²=9 B．（x+1）²+（y-2）²=9
C．（x-1）²+（y+2）²=3 D．（x+1）²+（y-2）²=3
组卷：502引用：10难度：0.8
解析
3．已知向量
a
=（2，1，-3），
b
=（1，-1，2），则
a
+2
b
=（　　）
A．3
2
B．（4，-1，1） C．（5，1，-4） D．
7
组卷：705引用：14难度：0.9
解析
4．点P是椭圆
x
2
2
+
y
2
5
=
1
上的动点，则P到椭圆两个焦点的距离之和为（　　）
A．
2
2
B．
2
3
C．
2
5
D．
2
7
组卷：345引用：6难度：0.9
解析
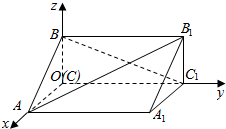5．如图，在空间直角坐标系中有直三棱柱ABC-A₁B₁C₁，CA=CC₁=2CB=2．则直线BC₁与直线AB₁夹角的余弦值为（　　）
A．
5
5
B．
5
3
C．
2
5
5
D．
3
5
组卷：77引用：3难度：0.7
解析
6．直线l：3x+4y-1=0被圆C：x²+y²-2x-4y-4=0所截得的弦长为（　　）
A．
2
5
B．4 C．
2
3
D．
2
2
组卷：1620引用：14难度：0.8
解析
7．已知椭圆
x
2
4
+
y
2
3
=
1
，F是椭圆的左焦点，P是椭圆上一点，若椭圆内一点A（1，1），则|PA|+|PF|的最小值为（　　）
A．3 B．
10
C．
5
+
1
2
D．
5
+
1
组卷：1407引用：8难度：0.8
解析

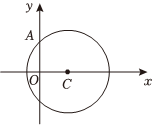21．已知圆C的圆心坐标为C（3，0），且该圆经过点A（0，4）．
（1）求圆C的标准方程；
（2）直线n交圆C于的M，N两点（点M，N异于A点），若直线AM，AN的斜率之积为2，求证：直线n过一个定点，并求出该定点坐标．
组卷：97引用：3难度：0.6
解析
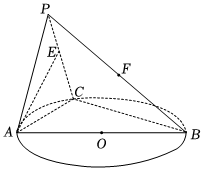22．如图，C是以AB为直径的圆O上异于A，B的点，平面PAC⊥平面ABC，△PAC为正三角形，E，F分别是PC，PB上的动点．
（1）求证：BC⊥AE；
（2）若E，F分别是PC，PB的中点且异面直线AF与BC所成角的正切值为
3
2
，记平面AEF与平面ABC的交线为直线l,点Q为直线l上动点，求直线PQ与平面AEF所成角的取值范围．
组卷：303引用：9难度：0.6
解析