2022-2023学年四川省南充一中三校区联考高三（上）月考数学试卷

一、单选题：本题共8小题，每小题5分，共40分.

• 1．直线x+1=0的倾斜角为（　　）

  A．0°

  B．45°

  C．90°

  D．不存在
  组卷：47引用：5难度：0.8

  解析

• 2．已知圆C：（x+1）²+（y-1）²=4，则圆心C与半径r分别为（　　）

  A．C（1，-1），r=4	B．C（-1，1），r=4
  C．C（1，-1），r=2	D．C（-1，1），r=2
  组卷：135引用：4难度：0.7

  解析

• 3．在棱长为1的正方体ABCD-A₁B₁C₁D₁中，异面直线AC与BD₁所成的角为（　　）

  A． π 4

  B． π 3

  C． π 2

  D． π 6
  组卷：116引用：6难度：0.7

  解析

• 4．已知点P（-5，12），Q是圆O：x²+y²=4上的动点，则线段PQ长的最小值为（　　）

  A．14

  B．13

  C．12

  D．11
  组卷：5引用：1难度：0.7

  解析

• 5．设m,n是两条不同的直线，α，β是两个不同的平面，则下列说法正确的是（　　）

  A．若m∥β，β⊥α，则m⊥α	B．若m⊥n,n⊥β，β⊥α，则m⊥α
  C．若m∥α且n∥α，则m∥n	D．若m⊥β，n⊥β，n⊥α，则m⊥α
  组卷：55引用：6难度：0.7

  解析

• 6．如图，二面角α-l-β等于135°，A，B是棱l上两点，BD，AC分别在半平面α，β内，AC⊥l,BD⊥l,且AB=AC=2，

  BD

  =

  2

  ，则CD=（　　）

  A． 2 3

  B． 2 2

  C． 14

  D．4
  组卷：201引用：8难度：0.5

  解析

• 7．蹴鞠，又名“蹴球”“蹴圆”等，“蹴“有用脚蹴、踢的含义，“鞠”最早系外包皮革、内饰米糠的球，因而“蹴鞠”就是指古人以脚蹴、踢皮球的活动，类似今日的踢足球活动．已知某“鞠”的表面上有四个点P、A、B、C，其中PA⊥平面ABC，PA=2

  2

  ，AB=AC=2，∠BAC=90°，则该球的体积为（　　）

  A．16π

  B． 16 π 3

  C． 32 π 3

  D．8π
  组卷：177引用：10难度：0.5

  解析

四、解答题：本题共6小题，其中17题10分，18、19、20、21、22题12分，共70分.

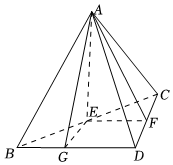• 21．如图，在三棱锥A-BCD中，△ABC是正三角形，平面ABC⊥平面BCD，BD⊥CD，点E，F分别是BC，DC的中点．
  （1）证明：平面ACD⊥平面AEF；
  （2）若∠BCD=60°，点G是线段BD上的动点，问：点G运动到何处时，平面AEG与平面ACD所成的锐二面角最小．
  组卷：420引用：12难度：0.6

  解析

• 22．古希腊数学家阿波罗尼奥斯的著作《圆锥曲线论》中给出圆的另一种定义：平面内，到两个定点距离之比值为常数λ（λ＞0，λ≠1）的点的轨迹是圆，我们称之为阿波罗尼奥斯圆．已知点P到A（-2，0）的距离是点P到B（1，0）的距离的2倍．
  （1）求点P的轨迹方程；
  （2）若点P与点Q关于点B对称，点C（5，8），求|QB|²+|QC|²的最大值；
  （3）若过B的直线与第二问中Q的轨迹交于E，F两点，试问在x轴上是否存在点M（m,0），使

  ME

  •

  MF

  恒为定值？若存在，求出点M的坐标和定值；若不存在，请说明理由．
  组卷：48引用：3难度：0.5

  解析