2022-2023学年江苏省南京市高三（上）学情调研数学试卷（7月预演）

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．若|1+iz|=|3+4i|，则|z-i|=（　　）

  A．2

  B．3

  C．4

  D．5
  组卷：54引用：2难度：0.8

  解析

• 2．若集合U=N^*，M={x∈N*|y=tan

  π

  2

  x}，N={y|y=x+

  4

  x

  ，

  1

  2

  ≤x≤4}，则（∁_UM）∩N=（　　）

  A．{5，7}

  B．{4，5，6，7}

  C．[4，8]

  D． [ 4 ， 17 2 ]
  组卷：47引用：3难度：0.6

  解析

• 3．在△ABC中，记

  CA

  =

  m

  ，

  CB

  =

  n

  ，则

  AB

  •

  （

  CA

  +

  CB

  ）

  =（　　）

  A． m - n

  B． m + n

  C． n 2 - m 2

  D． m 2 + n 2
  组卷：17引用：3难度：0.7

  解析

• 4．在△ABC中，AB=

  5

  ，

  AC

  =

  2

  ，BC=3．则以BC为轴，将△ABC旋转一周所得的几何体的体积为（　　）

  A． π 3

  B． 2 π 3

  C．π

  D． 4 π 3
  组卷：50引用：3难度：0.6

  解析

• 5．从1至8的8个整数中随机抽取2个不同的数，则这2个数和为偶数的概率为（　　）

  A． 11 14

  B． 5 14

  C． 4 7

  D． 3 7
  组卷：83引用：3难度：0.9

  解析

• 6．已知函数f（x）=sin（x+

  π

  9

  ）+sin（

  5

  π

  9

  -x），g（x）=f（f（x）），则g（x）的最大值为（　　）

  A． 2

  B． 3

  C． 3 2

  D．2
  组卷：111引用：3难度：0.6

  解析

• 7．双曲线C：

  x

  2

  a

  2

  -

  y

  2

  =1（a＞0）的左、右焦点分别为F₁，F₂，A为C左支上一动点，直线AF₂与C的右支交于点B，且|AB|=3a,△ABF₁与△BF₁F₂的周长相等，则|F₁F₂|=（　　）

  A． 2 3 3

  B． 4 3 3

  C． 2 3

  D． 4 3
  组卷：230引用：3难度：0.7

  解析

四、解答题：本题共6小题，共70分，解答时应写出文字说明，证明过程或演算步骤.

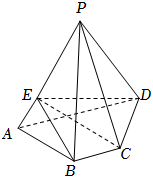• 21．如图，四棱锥P-ABCD的体积为

  3

  4

  ，平面PAD⊥平面ABCD，△PAD是面积为

  3

  的等边三角形，四边形ABCD是等腰梯形，BC=1，E为棱PA上一动点．
  （1）若直线EC与平面ABCD的夹角为60°，求二面角B-CE-D的正弦值；
  （2）求

  ED

  EC

  的取值范围．
  组卷：95引用：2难度：0.6

  解析

• 22．已知函数f（x）=

  ax

  e

  x

  和g（x）=

  lnx

  ax

  有相同的最大值．
  （1）求a；
  （2）证明：存在直线y=b,其与两条曲线y=f（x）和y=g（x）共有三个不同的交点，并且从左到右的三个交点的横坐标成等比数列．
  组卷：282引用：6难度：0.4

  解析