当前位置：试卷中心 > 试卷详情

2022-2023学年山东省淄博一中高二（下）第三次质检数学试卷

发布：2024/7/3 8:0:9

1．若i为虚数单位，则复数
z
=
2
-
i
1
-
i
的虚部为（　　）
A．
-
1
2
B．
-
1
2
i
C．
1
2
i
D．
1
2
组卷：108引用：9难度：0.8
解析
2．某地8名新冠肺炎病患者的潜伏期（单位：天）分别为7，8，8，12，11，10，14，16，则它们的75%分位数是（　　）
A．12 B．13 C．14 D．15
组卷：121引用：4难度：0.9
解析
3．一个扇形的圆心角为120°，面积为3π，则该扇形弧长为（　　）
A．π B．2π C．3π D．4π
组卷：83引用：2难度：0.7
解析
4．已知ABCD是平行四边形，
AE
=
2
EB
，若
EC
=
λ
AB
+
μ
AD
，则λ+μ=（　　）
A．
2
3
B．1 C．
4
3
D．
3
2
组卷：166引用：4难度：0.9
解析
5．设a=
1
2
cos6°-
3
2
sin6°，b=
2
tan
13
°
1
-
tan
2
13
°
，c=
1
-
cos
50
°
2
，则有（　　）
A．a＞b＞c B．a＜b＜c C．a＜c＜b D．b＜c＜a
组卷：352引用：18难度：0.7
解析
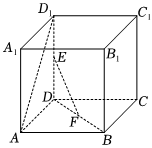6．如图，正方体ABCD-A₁B₁C₁D₁中，E，F分别是DD₁，DB的中点，则异面直线EF与AD₁所成角的正切值为（　　）
A．
2
B．
2
2
C．
3
3
D．
3
组卷：731引用：7难度：0.8
解析
7．已知圆台的上底面半径为2，下底面半径为4，若该圆台的体积为56π，则其母线长为（　　）
A．
2
10
B．
2
6
C．4 D．
13
组卷：237引用：5难度：0.7
解析

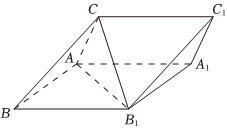21．如图，三棱柱ABC-A₁B₁C₁中、四边形ABB₁A₁是菱形，且∠ABB₁=60°，AB=BC=2，CA=CB₁，CA⊥CB₁，
（1）证明：平面CAB₁⊥平面ABB₁A₁；
（2）求直线BB₁和平面ABC所成角的正弦值；
组卷：625引用：8难度：0.6
解析
22．如图，△ABC的面积为8，记内角A，B，C所对的边分别为a,b,c,已知b=8，
8
cos
C
+
ccos
B
=
2
acos
∠
BAC
．
（1）求c的值；
（2）已知点M在线段AC上，点N为BC的中点，若
∠
ANM
=
π
4
，求sin∠AMN．
组卷：11引用：2难度：0.4
解析

1．若i为虚数单位，则复数z=2-i1-i的虚部为（ ）