当前位置：试卷中心 > 试卷详情

2023-2024学年广东省佛山市顺德区华侨中学高三（上）月考数学试卷（8月份）

发布：2024/8/6 8:0:9

一、单选题（每小题5分）

1．已知U=R，A={x|-1＜x＜3}，B={x|x≤2}，则∁_U（A∪B）=（　　）
A．（-∞，-1]∪（2，+∞） B．（-∞，-1）∪[2，+∞）
C．[3，+∞） D．（3，+∞）
组卷：441引用：10难度：0.8
解析
2．已知复数z满足（z+2i）（2-i）=5，则z的共轭复数
z
=（　　）
A．2-i B．2+i C．-2+i D．-2-i
组卷：119引用：7难度：0.8
解析
3．若
（
x
+
2
）
4
=
a
4
x
4
+
a
3
x
3
+
a
2
x
2
+
a
1
x
+
a
0
，则a₄-a₃+a₂-a₁+a₀=（　　）
A．1 B．-1 C．15 D．-15

组卷：240引用：4难度：0.9
解析
4．已知曲线y=axe^x+lnx在点（1，ae）处的切线方程为y=3x+b,则（　　）
A．a=e,b=-2 B．a=e,b=2 C．a=e^-1，b=-2 D．a=e^-1，b=2
组卷：518引用：13难度：0.7
解析
5．设公差不为零的等差数列{a_n}的前n项和为S_n，
a
4
=
1
2
a
5
，则
S
9
S
4
=（　　）
A．15 B．1 C．-1 D．-9
组卷：386引用：10难度：0.7
解析
6．现随机安排甲、乙等4位同学参加校运会跳高、跳远、投铅球比赛，要求每位同学参加一项比赛，每项比赛至少一位同学参加，事件A=“甲参加跳高比赛”，事件B=“乙参加跳高比赛”，事件C=“乙参加跳远比赛”，则（　　）
A．事件A与B相互独立 B．事件A与C为互斥事件
C．
P
（
C
|
A
）
=
5
12
D．
P
（
B
|
A
）
=
1
9
组卷：456引用：21难度：0.5
解析
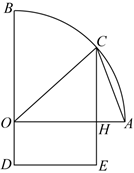7．如图，已知OAB是半径为2km的扇形，OA⊥OB，C是弧AB上的动点，过点C作CH⊥OA，垂足为H，某地区欲建一个风景区，该风景区由△AOC和矩形ODEH组成，且OH=2OD，则该风景区面积的最大值为（　　）
A．
5
2
k
m
2
B．
11
4
k
m
2
C．3km² D．
17
8
k
m
2
组卷：171引用：3难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题

21．为了“让广大青少年充分认识到毒品的危害性，切实提升青少年识毒防毒拒毒意识”，我市组织开展青少年禁毒知识竞赛，团员小明每天自觉登录“禁毒知识竞赛APP”，参加各种学习活动，同时热衷于参与四人赛．每局四人赛是由网络随机匹配四人进行比赛，每题回答正确得20分，第1个达到100分的比赛者获得第1名，赢得该局比赛，该局比赛结束．每天的四人赛共有20局，前2局是有效局，根据得分情况获得相应名次，从而得到相应的学习积分，第1局获得第1名的得3分，获得第2、3名的得2分，获得第4名的得1分；第2局获得第1名的得2分，获得第2、3、4名的得1分；后18局是无效局，无论获得什么名次，均不能获得学习积分．经统计，小明每天在第1局四人赛中获得3分、2分、1分的概率分别为
1
4
，
1
2
，
1
4
，在第2局四人赛中获得2分、1分的概率分别为
1
4
，
3
4
．
（1）设小明每天获得的得分为X，求X的分布列和数学期望；
（2）若小明每天赛完20局，设小明在每局四人赛中获得第1名从而赢得该局比赛的概率为
1
4
，每局是否赢得比赛相互独立，请问在每天的20局四人赛中，小明赢得多少局的比赛概率最大？
组卷：72引用：2难度：0.6
解析
22．已知函数f（x）=e^x-ax,g（x）=ln（x+2）-a,其中e为自然对数的底数，a∈R．
（1）当a＞0时，函数f（x）有极小值f（1），求a；
（2）证明：f'（x）＞g（x）恒成立；
（3）证明：
ln
2
+
（
ln
3
2
）
2
+
（
ln
4
3
）
3
+
…
+
（
ln
n
+
1
n
）
n
＜
e
e
-
1
．
组卷：657引用：4难度：0.6
解析

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A．（-∞，-1]∪（2，+∞）	B．（-∞，-1）∪[2，+∞）
C．[3，+∞）	D．（3，+∞）

A．事件A与B相互独立	B．事件A与C为互斥事件
C． P （ C \| A ） = 5 12	D． P （ B \| A ） = 1 9

2023-2024学年广东省佛山市顺德区华侨中学高三（上）月考数学试卷（8月份）

一、单选题（每小题5分）

1．已知U=R，A={x|-1＜x＜3}，B={x|x≤2}，则∁U（A∪B）=（ ）

2．已知复数z满足（z+2i）（2-i）=5，则z的共轭复数z=（ ）

3．若（x+2）4=a4x4+a3x3+a2x2+a1x+a0，则a4-a3+a2-a1+a0=（ ）

4．已知曲线y=axex+lnx在点（1，ae）处的切线方程为y=3x+b,则（ ）

5．设公差不为零的等差数列{an}的前n项和为Sn，a4=12a5，则S9S4=（ ）

6．现随机安排甲、乙等4位同学参加校运会跳高、跳远、投铅球比赛，要求每位同学参加一项比赛，每项比赛至少一位同学参加，事件A=“甲参加跳高比赛”，事件B=“乙参加跳高比赛”，事件C=“乙参加跳远比赛”，则（ ）

7．如图，已知OAB是半径为2km的扇形，OA⊥OB，C是弧AB上的动点，过点C作CH⊥OA，垂足为H，某地区欲建一个风景区，该风景区由△AOC和矩形ODEH组成，且OH=2OD，则该风景区面积的最大值为（ ）

四、解答题

22．已知函数f（x）=ex-ax,g（x）=ln（x+2）-a,其中e为自然对数的底数，a∈R．（1）当a＞0时，函数f（x）有极小值f（1），求a；（2）证明：f'（x）＞g（x）恒成立；（3）证明：ln2+（ln32）2+（ln43）3+…+（lnn+1n）n＜ee-1．

1．已知U=R，A={x|-1＜x＜3}，B={x|x≤2}，则∁_U（A∪B）=（　　）

2．已知复数z满足（z+2i）（2-i）=5，则z的共轭复数
z
=（　　）

3．若
（
x
+
2
）
4
=
a
4
x
4
+
a
3
x
3
+
a
2
x
2
+
a
1
x
+
a
0
，则a₄-a₃+a₂-a₁+a₀=（　　）

4．已知曲线y=axe^x+lnx在点（1，ae）处的切线方程为y=3x+b,则（　　）

5．设公差不为零的等差数列{a_n}的前n项和为S_n，
a
4
=
1
2
a
5
，则
S
9
S
4
=（　　）

6．现随机安排甲、乙等4位同学参加校运会跳高、跳远、投铅球比赛，要求每位同学参加一项比赛，每项比赛至少一位同学参加，事件A=“甲参加跳高比赛”，事件B=“乙参加跳高比赛”，事件C=“乙参加跳远比赛”，则（　　）

7．如图，已知OAB是半径为2km的扇形，OA⊥OB，C是弧AB上的动点，过点C作CH⊥OA，垂足为H，某地区欲建一个风景区，该风景区由△AOC和矩形ODEH组成，且OH=2OD，则该风景区面积的最大值为（　　）