2022-2023学年辽宁省铁岭市六校高二(下)期末数学试卷
发布:2024/7/3 8:0:9
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1.命题“∃x0∈N,
”的否定是( )ex0-x0-1≤0组卷:72引用:2难度:0.7 -
2.已知数列-6,66,-666,6666,-66666,…,则该数列的第2024项为( )
组卷:210引用:3难度:0.7 -
3.函数
的导数f′(x)=( )f(x)=cosxx组卷:265引用:4难度:0.8 -
4.若公比为-3的等比数列的前2项和为10,则该等比数列的第3项为( )
组卷:141引用:5难度:0.9 -
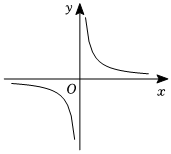 5.已知函数,g(x)=x2+1,则如图对应的函数解析式可能是( )f(x)=x+1x组卷:26引用:3难度:0.6
5.已知函数,g(x)=x2+1,则如图对应的函数解析式可能是( )f(x)=x+1x组卷:26引用:3难度:0.6 -
6.设Tn是数列{an}的前n项积,则“
”是“{an}是等差数列”的( )Tn=3n组卷:32引用:4难度:0.7 -
7.若存在直线y=kx+b,使得函数F(x)和G(x)对其公共定义域上的任意实数x都满足F(x)≥kx+b≥G(x),则称此直线y=kx+b为F(x)和G(x)的“隔离直线”.已知函数f(x)=x2,g(x)=alnx(a>0),若f(x)和g(x)存在唯一的“隔离直线”,则a=( )
组卷:149引用:3难度:0.5
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
-
21.已知公差为-2的等差数列{an}的前n项和为Sn,且S5=-5.
(1)求{an}的通项公式;
(2)若数列的前n项和为Tn,证明:{1anan+1}为定值.Tn-12an+1组卷:73引用:3难度:0.5 -
22.已知函数
.f(x)=32x2-x-xlnx
(1)求f(x)的图象在点(1,f(1))处的切线方程;
(2)证明:f(x)+cosx-1>0.组卷:40引用:2难度:0.4


