2022-2023学年福建省宁德一中高一（下）月考数学试卷（5月份）

一、单选题：本题共8小题，每小题5分，共40分

• 1．复数z满足（1-

  3

  i）z=|2i|，i为虚数单位，则复数z的虚部为（　　）

  A．- 3 3

  B． 3 3

  C．- 3 2

  D． 3 2
  组卷：302引用：5难度：0.7

  解析

• 2．设x∈R，向量

  a

  =（x,1），

  b

  =（1，-2），且

  a

  ∥

  b

  ，则|

  a

  +

  b

  |=（　　）

  A． 5 2

  B． 10 2

  C． 5

  D．5
  组卷：328引用：4难度：0.8

  解析

• 3．某中学的高一、高二、高三共有学生1350人，其中高一500人，高三比高二少50人，为了解该校学生健康状况，现采用分层抽样方法进行调查，在抽取的样本中有高一学生120人，则该样本中的高二学生人数为（　　）

  A．80

  B．96

  C．108

  D．110
  组卷：2152引用：11难度：0.5

  解析

• 4．已知α、β是空间中两个不同的平面，m、n是空间中两条不同的直线，则下列命题中正确的是（　　）

  A．若m∥n,n⊂α，则m∥α	B．若m∥α，m∥β，则α∥β
  C．若α⊥β，m⊂α，则m⊥β	D．若m⊥α，n⊥β，m⊥n,则α⊥β
  组卷：233引用：4难度：0.6

  解析

• 5．如图，AB是圆的直径，PA垂直于圆所在的平面，C是圆上一点（不同于A，B）且PA=AC，则二面角P-BC-A大小为（　　）

  A．60°

  B．30°

  C．45°

  D．15°
  组卷：849引用：7难度：0.5

  解析

• 6．埃及胡夫金字塔是古代世界建筑奇迹之一，它的形状可视为一个正四棱锥．以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积，则其侧面三角形底边上的高与底面正方形的边长的比值为（　　）

  A． 5 - 1 4

  B． 5 - 1 2

  C． 5 + 1 4

  D． 5 + 1 2
  组卷：7870引用：31难度：0.6

  解析

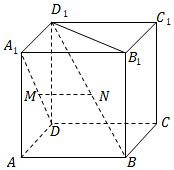• 7．如图，已知正方体ABCD-A₁B₁C₁D₁，M，N分别是A₁D，D₁B的中点，则（　　）

  A．直线A1D与直线D1B相交，直线MN∥平面ABCD

  B．直线A1D与直线D1B平行，直线MN⊥平面ABCD

  C．直线A1D与直线D1B垂直，直线MN∥平面ABCD

  D．直线A1D与直线D1B异面，直线MN⊥平面ABCD
  组卷：331引用：3难度：0.8

  解析

四、解答题：本题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤

• 21．四棱锥S-ABCD中，底面ABCD为平行四边形，侧面SBC⊥底面ABCD，已知∠ABC=45°，AB=2，BC=2

  2

  
  ，SA=SB=

  3

  ．​
  （Ⅰ）证明：SA⊥BC；
  （Ⅱ）求直线SD与平面SBC所成角的正弦值．
  组卷：100引用：1难度：0.6

  解析

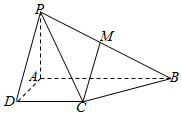• 22．已知四棱锥P-ABCD的底面为直角梯形，AB∥DC，∠DAB=90°，PA⊥平面ABCD，且PA=AD=DC=

  1

  2

  AB=1，M是棱PB上的动点．
  （1）求证：平面PAD⊥平面PCD；
  （2）若PD∥平面ACM，求

  PM

  MB

  的值；
  （3）当M是PB中点时，设平面ADM与棱PC交于点N，求截面ADNM的面积．
  组卷：478引用：2难度：0.3

  解析