当前位置：试卷中心 > 试卷详情

2023年西藏林芝第二高级中学高考数学四模试卷（理科）

发布：2024/7/26 8:0:9

1．设集合A={x|-1≤x＜3}，B={1，2，3，4}，则A∩B=（　　）
A．{1} B．{1，2} C．{2，3} D．{1，2，3}
组卷：305引用：7难度：0.8
解析
2．已知复数
z
=
2
-
i
1
+
i
，则
z
-
z
=（　　）
A．3i B．-3i C．3 D．-3
组卷：34引用：2难度：0.8
解析
3．已知命题p：∀x＞0，总有（x+1）e^x＞1，则￢p为（　　）
A．∃x₀≤0，使得（x₀+1）
e
x
0
≤1
B．∃x₀＞0，使得（x₀+1）
e
x
0
≤1
C．∀x₀＞0，使得（x₀+1）
e
x
0
≤1
D．∀x₀≤0，使得（x₀+1）
e
x
0
≤1
组卷：570引用：17难度：0.9
解析
4．已知向量
a
=（1，2），
b
=（-2，t），若
a
∥
b
，则t=（　　）
A．-4 B．1 C．2 D．4
组卷：850引用：17难度：0.8
解析
5．已知函数
f
（
x
）
=
2
x
2
+
1
，
x
≤
1
2
x
-
2
，
x
＞
1
，则f（f（2））=（　　）
A．5 B．3 C．2 D．1
组卷：94引用：4难度：0.8
解析
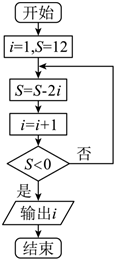
6．执行如图所示的算法框图，则输出的l的值为（　　）
A．4 B．5 C．6 D．7
组卷：14引用：4难度：0.7
解析
7．
f
（
x
）
=
e
x
x
2
的图像大致是（　　）
A． B． C． D．
组卷：74引用：3难度：0.8
解析

22．在平面直角坐标系xOy中，曲线C的参数方程为
x
=
2
+
4
cosα
，
y
=
4
sinα
（α为参数），以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，直线l的极坐标方程是ρcosθ-ρsinθ-3=0．
（1）求曲线C的直角坐标方程和直线l的普通方程；
（2）若P（0，-3），直线l与曲线C交于A，B两点，M是线段AB的中点，求
|
PM
|
|
PA
|
+
|
PB
|
的值．
组卷：189引用：9难度：0.6
解析
23．已知函数f（x）=|2x-1|+|x|-x+2．
（1）求不等式f（x）≥3的解集；
（2）设函数y=f（x）的值域为M，a,b∈M，试比较ab+2与2a+b的大小．
组卷：14引用：4难度：0.5
解析