2023-2024学年福建省厦门十一中九年级（上）开学数学试卷

一、选择题（每小题4分，共40分。其中有且只有一个选项正确）

• 1．一元二次方程x²+6x+9=0的常数项是（　　）

  A．0

  B．1

  C．6

  D．9
  组卷：876引用：8难度：0.9

  解析

• 2．已知代数式

  x

  -

  3

  有意义，则x的值可能是（　　）

  A．4

  B．2

  C．1

  D．0
  组卷：119引用：4难度：0.7

  解析

• 3．已知y是x的函数，且当x=1时，y=-1，那么该函数的解析式可以是（　　）

  A．y=x

  B．y=-2x

  C．y=x-2

  D．y=-x+2
  组卷：606引用：3难度：0.5

  解析

• 4．将抛物线y=x²通过一次平移可得抛物线y=x²-5，对此平移过程描述正确的是（　　）

  A．向上平移5个单位长度	B．向下平移5个单位长度
  C．向左平移5个单位长度	D．向右平移5个单位长度
  组卷：131引用：3难度：0.8

  解析

• 5．某校举行年度十佳校园歌手大赛，林老师根据七位评委所给的分数，把最后一位参赛同学的得分制作成如下表格，对七位评委所给的分数，如果去掉一个最高分和一个最低分，那么表中数据一定不会发生变化的是（　　）
  

  平均数	中位数	众数	方差
  88.5分	86分	87分	5.6

  A．平均数

  B．中位数

  C．众数

  D．方差
  组卷：99引用：5难度：0.7

  解析

• 6．某开发公司2021年投入的研发资金为100亿元，为了扩大产品的竞争力，该公司不断增加研发投资，计划2023年投入400亿元研发资金．若2021年到2023年投入的研发资金年平均增长率均为x,则下列方程中正确的是（　　）

  A．100（1+x）=400

  B．100（1+2x）=400

  C．100（1+x）+100（1+x）2=400

  D．100（1+x）2=400
  组卷：362引用：7难度：0.6

  解析

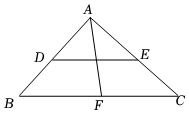• 7．如图，在Rt△ABC中，∠BAC=90°，D、E、F分别是三边的中点，AF=5，则DE的长为（　　）

  A．2.5

  B．4

  C．5

  D．10
  组卷：197引用：6难度：0.6

  解析

• 8．如图是二次函数y=ax²+bx+c的图象，图象上有两点分别为A（2.18，-0.51），B（2.68，0.54），则方程ax²+bx+c=0的一个解有可能是（　　）

  A．2.18

  B．2.68

  C．-0.51

  D．2.45
  组卷：232引用：3难度：0.7

  解析

三、解答题（本大题有9小题，共86分，解答应写出必要的文字说明、演算步骤或推理过程。）

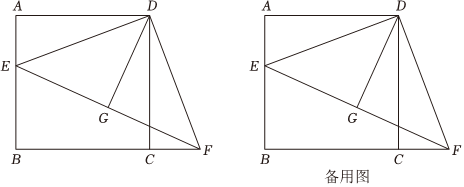• 24．如图，正方形ABCD中，点E在AB上，点F在BC延长线上，且AE=CF，连接DE、DF、EF，作EF的中点G．
  （1）求证△DAE≌△DCF；
  （2）求证：A、G、C三点共线；
  （3）延长DG交BC于H，若BE=2AE，求证：BH=CH．
  组卷：103引用：2难度：0.3

  解析

• 25．“厚德楼”、“求真楼”分别是我校两栋教学楼的名字，“厚德”出自《周易大传》：天行健，君子以自强不息；地势坤，君子以厚德载物．“求真”出自《闽中理学渊源考》：“求真于未始有伪之先，而性之真可见矣．”我们不妨约定：在平面直角坐标系中，横、纵坐标相等的点称为“厚德点”，横、纵坐标互为相反数的点称为“求真点”．把函数图象至少经过一个“厚德点”和一个“求真点”的函数称为“厚德求真函数”．
  （1）函数y=2x-1是一个“厚德求真函数”，直接写出该函数图象上的“厚德点”和“求真点”；
  （2）已知二次函数y=a（x-h）²+k图象可以由二次函数y=-x²平移得到，二次函数y=a（x-h）²+k的顶点就是一个“厚德点”，并且该函数图象还经过一个“求真点”P（3，m），求该二次函数的解析式；
  （3）已知二次函数y=2（x-c）²+d （c,d为常数，c≠0）图象的顶点为M，与y轴交于点N，经过点M，N的直线l上存在无数个“厚德点”．当m-1≤x≤m,函数y=2（x-c）²+d有最小值

  15

  2

  ，求m的值．
  组卷：100引用：1难度：0.3

  解析