当前位置：试卷中心 > 试卷详情

2022-2023学年浙江省宁波市南三县八年级（下）期末数学试卷

发布：2024/6/13 8:0:9

一、选择题（本大题共10小题，共30分）

1．若式子
x
-
1
有意义，则x的值可以为（　　）
A．4 B．-4 C．-1 D．0
组卷：91引用：5难度：0.9
解析
2．下列航天图标，其文字上方的图案是中心对称图形的是（　　）
A．
中国探火 B．
中国火箭
C．
中国行星探测 D．
航天神舟
组卷：83引用：7难度：0.5
解析
3．下列方程一定是一元二次方程的是（　　）
A．2x-1=4x+3 B．2x²+y-1=0 C．2x²-1=3 D．ax²+bx+c=0
组卷：492引用：8难度：0.9
解析
4．用反证法证明命题“在同一平面内，若a⊥b,c⊥b,则a∥c”时，首先应假设（　　）
A．a∥b B．c∥b C．a与c相交 D．a与b相交
组卷：511引用：10难度：0.7
解析
5．菱形具有而矩形不一定具有的性质是（　　）
A．对角相等 B．邻角互补
C．对角线互相平分 D．对角线平分一组对角
组卷：114引用：2难度：0.7
解析
6．若一元二次方程x²-2x+k=0有两个不相等的实数根，则k的取值范围是（　　）
A．k＞1 B．k＜1 C．k＜1且k≠0 D．k≥1
组卷：1022引用：8难度：0.9
解析
7．一场有19位同学参加的比赛，取前10名进决赛且所得分数互不相同．某同学知道自己的分数后要判断是否能进决赛，他只需要知道这19位同学所得分数的（　　）
A．平均数 B．中位数 C．众数 D．方差
组卷：61引用：2难度：0.7
解析
8．以下函数在自变量的取值范围内y随x的增大而减小的是（　　）
A．y=2x-1 B．
y
=
1
3
x
C．
y
=
-
3
x
（
x
＜
0
）
D．
y
=
6
x
（
x
＞
0
）
组卷：363引用：3难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本大题共8小题，共66分）

23．阅读材料，根据上述材料解决以下问题：
材料1：若一元二次方程 ax²+bx+c=0（a≠0）的两个根为 x₁x₂，则
x
1
+
x
2
=
-
b
a
x
1
x
2
=
c
a

材料2：已知实数m,n满足 m²-m-1=0，n²-n-1=0，且m≠n,则 m,n 是方程x²-x-1=0 的两个不相等的实数根．
（1）材料理解：一元二次方程 3x²-6x+1=0 两个根为 x₁x₂，则 x₁+x₂=
，x₁x₂=
．
（2）应用探究：已知实数m,n满足 9m²-9m-1=0，9n²-9n-1=0，且m≠n,求 m²n+mn²的值．
（3）思维拓展：已知实数s、t分别满足 9s²+9s+1=0，t²+9t+9=0，其中st≠1且st≠0．求
3
st
+
9
s
+
3
t
的值．
组卷：724引用：1难度：0.5
解析
24．定义：把能被一条对角线分成两个全等直角三角形的四边形叫做勾股四边形．
（1）矩形
勾股四边形（填“是”或“不是”）．
（2）如图在直角坐标系xOy中，直线y=-x+1与双曲线
y
=
-
6
x
相交于A，B两点，点P（-3，0）在x轴负半轴上，Q为直角坐标平面上一点．
①分别求出A、B两点的坐标．
②当四边形APQB是平行四边形时，如图（Ⅰ），请证明▱APQB是勾股四边形．
（3）在（2）的条件下，当以A、B、P、Q为顶点的四边形是勾股四边形时，请直接写出Q点的坐标．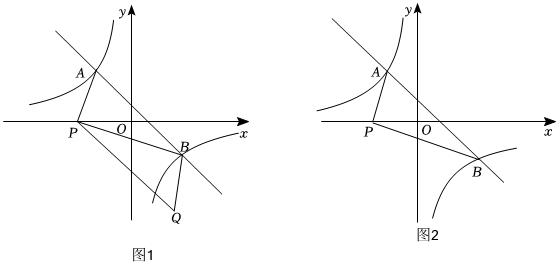

组卷：617引用：3难度：0.5
解析