2022-2023学年安徽省六安一中高二（下）期末数学试卷

一、单项选择题：本大题8个小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的。

• 1．已知集合A={x|x²+x-2≤0}，

  B

  =

  {

  x

  |

  x

  -

  2

  x

  +

  1

  ≥

  0

  }

  ，则A∩B=（　　）

  A．{x|-2≤x≤2}

  B．{x|-2≤x≤1}

  C．{x|-2≤x≤-1}

  D．{x|-2≤x＜-1}
  组卷：132引用：3难度：0.8

  解析

• 2．若x,y,z为非零实数，则“x＜y＜z”是“x+y＜2z”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分也不必要条件
  组卷：101引用：5难度：0.7

  解析

• 3．已知函数y=log_a（x-3）+2（a＞0且a≠1）的图象恒过定点P，点P在幂函数y=f（x）的图象上，则f（4）=（　　）

  A．-2

  B．2

  C．1

  D．-1
  组卷：135引用：3难度：0.7

  解析

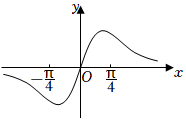• 4．已知函数f（x）=e^x+e^-x，g（x）=sinx,则图象为如图的函数可能是（　　）

  A． y = g （ x ） f （ x ）	B． y = f （ x ） - g （ x ） - 1 4
  C． y = f （ x ） g （ x ）	D． y = f （ x ） + g （ x ） - 1 4
  组卷：92引用：3难度：0.7

  解析

• 5．用模型y=ae^kx拟合一组数（x_i，y_i）（i=1，2，…，10），若x₁+x₂+…+x₁₀=10，

  y

  1

  y

  2

  …

  y

  10

  =

  e

  70

  ，设z=lny,得变换后的线性回归方程为

  ̂

  z

  =

  ̂

  b

  x

  +

  4

  ，则ak=（　　）

  A．12

  B．3e4

  C．4e3

  D．7
  组卷：153引用：4难度：0.7

  解析

• 6．已知函数f（x）是定义在实数集R上的不恒为零的偶函数，且对任意实数x都有xf（x+1）=（1+x）f（x），则f（

  5

  2

  ）的值是（　　）

  A．0

  B． 1 2

  C．1

  D． 5 2
  组卷：1158引用：67难度：0.3

  解析

• 7．2023年1月底，人工智能研究公司OpenAI发布的名为“ChatGTP”的人工智能聊天程序进入中国，迅速以其极高的智能化水平引起国内关注．深度学习是人工智能的一种具有代表性的实现方法，它是以神经网络为出发点的，在神经网络优化中，指数衰减的学习率模型为

  L

  =

  L

  0

  D

  G

  G

  0

  ，其中L表示每一轮优化时使用的学习率，L₀表示初始学习率，D表示衰减系数，G表示训练迭代轮数，G₀表示衰减速度．已知某个指数衰减的学习率模型的初始学习率为0.8，衰减速度为12，且当训练迭代轮数为12时，学习率衰减为0.5．则学习率衰减到0.2以下（不含0.2）所需的训练迭代轮数至少为（　　）（参考数据：lg2≈0.3010）

  A．36

  B．37

  C．38

  D．39
  组卷：134引用：3难度：0.5

  解析

四．解答题：本小题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤．

• 21．已知函数f（x）=（a+1）e^x-ax（a∈R）．
  （1）讨论f（x）的单调性；
  （2）若x＜0，f（x）≥-x²-x-1，求实数a的取值范围．
  组卷：33引用：2难度：0.3

  解析

• 22．最新研发的某产品每次试验结果为成功或不成功，且试验成功的概率为p（0＜p＜1）．现对该产品进行独立重复试验，若试验成功，则试验结束；若试验不成功，则继续试验，且最多试验10次．记X为试验结束时所进行的试验次数．
  （1）写出X的分布列；
  （2）证明：

  E

  （

  X

  ）

  ＜

  1

  p

  ．
  组卷：188引用：2难度：0.3

  解析