2023-2024学年河北省衡水二中高二（上）第四次调研数学试卷

一、单项选择题：本题共8小愿，每题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．双曲线

  x

  2

  a

  +

  1

  -

  y

  2

  1

  =

  1

  与椭圆

  x

  2

  4

  +

  y

  2

  a

  2

  =

  1

  的焦点相同，则a等于（　　）

  A．1

  B．-2

  C．1或-2

  D．2
  组卷：172引用：2难度：0.7

  解析

• 2．已知双曲线

  x

  2

  a

  +

  y

  2

  =

  1

  的一条渐近线倾斜角为

  5

  π

  6

  ，则a=（　　）

  A．±3

  B． ± 1 3

  C．3

  D．-3
  组卷：128引用：2难度：0.8

  解析

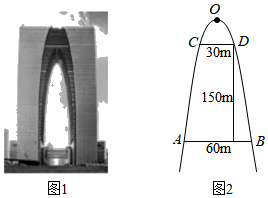• 3．苏州市“东方之门”是由两栋超高层建筑组成的双塔连体建筑，“门”的造型是东方之门的立意基础，“门”的内侧曲线呈抛物线型，如图1，两栋建筑第八层由一条长60m的连桥连接，在该抛物线两侧距连桥150m处各有一窗户，两窗户的水平距离为30m,如图2，则此抛物线顶端O到连桥AB距离为（　　）

  A．180m

  B．200m

  C．220m

  D．240m
  组卷：178引用：7难度：0.8

  解析

• 4．已知F₁，F₂分别是双曲线

  C

  ：

  x

  2

  -

  y

  2

  2

  =

  1

  的左、右两个焦点，点M在双曲线的右支上，且|MF₁|+|MF₂|=6，则∠MF₁F₂=（　　）

  A．30°

  B．45°

  C．60°

  D．90°
  组卷：173引用：6难度：0.5

  解析

• 5．过椭圆

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  左焦点F作x轴的垂线，交椭圆于P，Q两点，A是椭圆与x轴正半轴的交点，且|PQ|=|FA|，则该椭圆的离心率是（　　）

  A． 1 2

  B． 2 4

  C． 2 2

  D． 3 2
  组卷：589引用：7难度：0.8

  解析

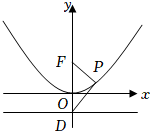• 6．如图，抛物线E：x²=2py（p＞0）的焦点为F，准线与y轴交于点D，O为坐标原
  点，P是抛物线上一点，且∠PFO=60°，则

  |

  PF

  |

  |

  DF

  |

  =（　　）

  A． 2 7 3

  B． 7 2

  C． 7 3

  D． 2 3
  组卷：59引用：4难度：0.6

  解析

• 7．已知抛物线C：y²=2px（p＞0）的焦点为F，点T在C上，且|FT|=

  5

  2

  ，若点M的坐标为（0，1），且MF⊥MT，则C的方程为（　　）

  A．y2=2x或y2=8x	B．y2=x或y2=8x
  C．y2=2x或y2=4x	D．y2=x或y2=4x
  组卷：395引用：4难度：0.6

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明，证明过程或演算步骤.

• 21．已知椭圆

  E

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的长轴长为4，且点

  P

  （

  1

  ，

  3

  2

  ）

  在椭圆E上．
  （1）求椭圆E的方程；
  （2）过椭圆E的右焦点F作不与两坐标轴重合的直线l,与E交于不同的两点M，N，线段MN的中垂线与y轴相交于点T，求

  |

  MN

  |

  |

  OT

  |

  （O为原点）的最小值，并求此时直线l的方程．
  组卷：65引用：2难度：0.3

  解析

• 22．若M（

  p

  2

  ，p）为抛物线y²=2px（p＞0）上一点，M到点（1，0）的距离比到y轴的距离大1，
  （1）求抛物线的方程
  （2）作直线l与抛物线相交于A．B两点，以AB为直径的圆过点M，求点（1，0）到直线l的距离的最大值．
  组卷：6引用：2难度：0.5

  解析