2023-2024学年广东省广州一中高二(上)月考数学试卷(10月份)
发布:2024/9/9 3:0:9
一、单选题(本大题共8小题,共40.0分.在每小题列出的选项中,选出符合题目的一项)
-
1.已知过点A(1,a),
的直线的倾斜角为60°,则实数a的值为( )B(2,-3)组卷:237引用:5难度:0.7 -
2.下列说法错误的是( )
组卷:357引用:13难度:0.8 -
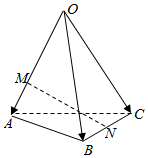 3.如图,空间四边形OABC中,,点M在OA=a,OB=b,OC=c上,且OM=2MA,点N为BC中点,则OA=( )MN组卷:2461引用:155难度:0.9
3.如图,空间四边形OABC中,,点M在OA=a,OB=b,OC=c上,且OM=2MA,点N为BC中点,则OA=( )MN组卷:2461引用:155难度:0.9 -
4.已知
,a=(1,0,1),且b=(x,1,-2),则向量a•b=-3与a的夹角为( )b组卷:690引用:7难度:0.7 -
5.已知
=(2,1,-3),a=(-1,2,3),b=(7,6,λ),若c,a,b共面,则λ等于( )c组卷:660引用:18难度:0.8 -
 6.在平行六面体ABCD-A1B1C1D1中,底面ABCD是菱形,侧面A1ADD1是正方形,且∠A1AB=120°,∠DAB=60°,AB=2,若P是C1D与CD1的交点,M是A1D1的中点,则MP=( )组卷:93引用:5难度:0.5
6.在平行六面体ABCD-A1B1C1D1中,底面ABCD是菱形,侧面A1ADD1是正方形,且∠A1AB=120°,∠DAB=60°,AB=2,若P是C1D与CD1的交点,M是A1D1的中点,则MP=( )组卷:93引用:5难度:0.5 -
7.三棱锥P-ABC中,△PAB和△ABC都是等边三角形,AB=2,PC=1,D为棱AB上一点,则
的值为( )PD•PC组卷:177引用:7难度:0.6
四、解答题(本大题共6小题,共70.0分.解答应写出文字说明,证明过程或演算步骤)
-
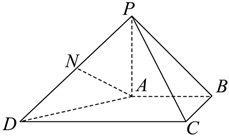 21.如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB∥CD,且AB=1,CD=2,,PA=1,AB⊥BC,N为PD的中点.BC=22
21.如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB∥CD,且AB=1,CD=2,,PA=1,AB⊥BC,N为PD的中点.BC=22
(1)求证:AN∥平面PBC;
(2)求平面PDC与平面PBC夹角的余弦值.组卷:259引用:4难度:0.6 -
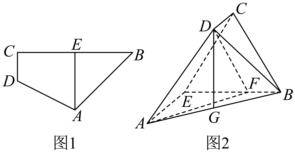 22.如图1,在四边形ABCD中,BC⊥CD,AE∥CD,AE=BE=2CD=2,CE=.将四边形AECD沿AE折起,使得BC=3,得到如图2所示的几何体.3
22.如图1,在四边形ABCD中,BC⊥CD,AE∥CD,AE=BE=2CD=2,CE=.将四边形AECD沿AE折起,使得BC=3,得到如图2所示的几何体.3
(1)若G为AB的中点,证明:DG⊥平面ABE;
(2)若F为BE上一动点,且二面角B-AD-F的余弦值为,求63的值.EFEB组卷:134引用:4难度:0.4


