当前位置：试卷中心 > 试卷详情

2022-2023学年福建省厦门外国语学校瑞景分校九年级（上）期中数学试卷

发布：2024/9/16 13:0:8

一、选择题（本大题共10小题。每小题4分。共40分。每小题只有一项符合题意）

1．抛物线y=2（x-1）²+6的顶点坐标是（　　）
A．（1，-6） B．（-1，-6） C．（1，6） D．（-1，6）
组卷：207引用：7难度：0.8
解析
2．下列关于防范“新冠肺炎”的标志中是中心对称图形的是（　　）
A．
戴口罩讲卫生 B．
勤洗手勤通风
C．
有症状早就医 D．
少出门少聚集
组卷：79引用：4难度：0.8
解析
3．如图是抛物线y=ax²+bx+c的示意图，则c的值可以是（　　）
A．-2 B．-1 C．0 D．3
组卷：22引用：3难度：0.7
解析
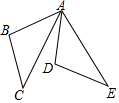4．如图△ABC绕点A旋转至△ADE，则旋转角是（　　）
A．∠BAD B．∠BAC C．∠BAE D．∠CAD
组卷：596引用：15难度：0.8
解析
5．下列一元二次方程中，没有实数根的是（　　）
A．x²+12x=0 B．x（x-1）=0 C．x²+1=0 D．x²+x=1
组卷：10引用：2难度：0.7
解析
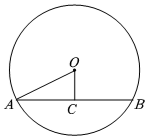6．如图，在⊙O中，弦AB=4，圆心O到AB的距离OC=1，则⊙O的半径长为（　　）
A．2
5
B．2
3
C．
5
D．
3
组卷：397引用：10难度：0.7
解析
7．有一人患了流感，经过两轮传染后，共有121人患了流感，每轮传染中平均每人传染了x个人，下列结论错误的是（　　）
A．1轮后有（x+1）个人患了流感
B．2轮后有（x+1）•x个人患流感
C．依题意可得方程（x+1）²=121
D．不考虑其他因素经过三轮一共会有1331人感染
组卷：60引用：2难度：0.5
解析
8．汽车刹车后行驶的距离s（单位：m）关于行驶时间t（单位：s）的函数解析式是s=15t-6t²，则行驶时间t的取值范围是（　　）
A．t≥0 B．
0
≤
t
≤
5
4
C．
5
4
≤
t
≤
5
2
D．
0
≤
t
≤
5
2
组卷：57引用：2难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本大题共9小题。共86分、解答应写出文字说明、证明过程或演算步骤。）

24．对于一个四边形给出如下定义：有一组对角相等且有一组邻边相等，则称这个四边形为奇特四边形．
（1）判断命题“另一组邻边也相等的奇特四边形为正方形”是真命题还是假命题？
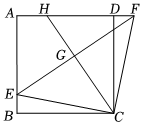
（2）如图，在正方形ABCD中，E是AB边上一点，F是AD延长线一点，BE=DF，连接EF，EC，FC，取EF的中点G，连接CG并延长交AD于点H．探究：四边形BCGE是否是奇特四边形，如果是证明你的结论，如果不是请说明理由．
（3）在（2）的条件下，若四边形BCGE的面积为16，则BC+BE的值是多少？
组卷：82引用：3难度：0.1
解析
25．已知，点M为二次函数y=x²+2bx+3c图象的顶点，一次函数y=kx-3（k＞0）分别交x轴，y轴于点A，B．
（1）若b=1，c=1，判断顶点M是否在直线y=2x+4上，并说明理由；
（2）若该二次函数图象经过点C（1，-4），也经过点A，B，且满足kx-3＜x²+2bx+3c.求该一次函数解析式，并直接写出自变量x的取值范围；
（3）设点P坐标为（m,n）在二次函数y=x²+2bx+3c上，当-2≤m≤2时，b-24≤n≤2b+4，试问：当b≥2或b≤-2时，对于该二次函数中任意的自变量x,函数值y是否始终大于-40？请说明理由．
组卷：58引用：2难度：0.5
解析