2023年河北省部分示范性高中高考数学三模试卷
发布:2024/6/19 8:0:9
一、单选题。(本题共8个小题,每小题5分,共40分)
-
1.已知集合A={x∈Z|x2+x>6},B={x|-4≤x≤4},则A∩B=( )
组卷:163引用:3难度:0.8 -
2.已知复数z满足:(2+i)z=m,(其中i为虚数单位,m为实数且m<0),则z的共轭复数
在复平面内对应的点位于( )z组卷:59引用:4难度:0.7 -
3.直线l1:ax+y+1=0 与l2:x+ay-1=0平行的充要条件是( )
组卷:280引用:1难度:0.7 -
4.现有一张长方形纸片,将其沿直线(不过顶点)剪开,得到2张纸片,再从中任选一张沿直线(不过顶点)剪开,得到3张纸片…,以此类推,每次从纸片中任选一张沿直线(不过顶点)剪开,设剪纸n次后得到的所有多边形的边数总和为an,则a1+a2+a3⋯+a10=( )
组卷:16引用:1难度:0.8 -
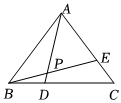 5.如图,在△ABC中,已知,BD=13BC,P是线段AD与BE的交点,若AE=23AC,则m+n的值为( )AP=mAB+nAC组卷:212引用:1难度:0.6
5.如图,在△ABC中,已知,BD=13BC,P是线段AD与BE的交点,若AE=23AC,则m+n的值为( )AP=mAB+nAC组卷:212引用:1难度:0.6 -
6.已知函数f(x)的定义域为R,函数g(x)=f(x)+x2为奇函数,且g(x+4)=g(x),则f(6)的值为( )
组卷:450引用:2难度:0.7 -
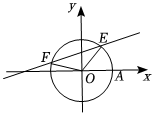 7.如图,在平面直角坐标系中,以OA为始边,角α与β的终边分别与单位圆相交于E,F两点,且,α∈(0,π2),若直线EF的斜率为β∈(π2,π),则sin(α+β)=( )14组卷:205引用:6难度:0.6
7.如图,在平面直角坐标系中,以OA为始边,角α与β的终边分别与单位圆相交于E,F两点,且,α∈(0,π2),若直线EF的斜率为β∈(π2,π),则sin(α+β)=( )14组卷:205引用:6难度:0.6
四、解答题。(本题共6个小题,共70分)
-
21.已知函数f(x)=xlnx-ax2+3x.
(1)若对任意的x∈(0,+∞),f(x)≤1恒成立,求实数a的取值范围;
(2)证明:当n∈N*时,.31×2+42×3+53×4+…+n+2n(n+1)≥ln(n+1)组卷:160引用:4难度:0.5 -
22.已知
.f(x)=a(x-lnx)+2x-1x2(a>0)
(1)讨论f(x)的单调性;
(2)当a=1时,证明对于任意的x∈[1,+∞)成立.f(x)>f′(x)+32组卷:68引用:3难度:0.2


