当前位置：试卷中心 > 试卷详情

2022-2023学年河北省衡水中学高三（上）第四次调研数学试卷

发布：2024/8/16 12:0:1

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．已知
z
=
i
（
3
-
i
）
2
+
i
，则z在复平面内对应的点位于（　　）
A．实轴上
B．虚轴上
C．第一、三象限的角平分线上
D．第二、四象限的角平分线上
组卷：1引用：2难度：0.8
解析
2．已知平面向量
a
，
b
满足
|
a
|
=
2
，
b
=
（
1
，
1
）
，
|
a
+
b
|
=
10
，则
a
在
b
上的投影向量的坐标为（　　）
A．
（
2
2
，
2
2
）
B．（1，1） C．（-1，-1） D．
（
-
2
2
，
2
2
）
组卷：559引用：15难度：0.8
解析
3．在直角三角形ABC中，A=90°，B=60°，AB=2，则
AB
•
BC
=（　　）
A．-4 B．4 C．-8 D．8
组卷：79引用：3难度：0.8
解析
4．设A，B，C为平面内任意三点，则“
AB
与
AC
的夹角为钝角”是“|
AB
+
AC
|＜|
BC
|”的（　　）
A．必要不充分条件 B．充分不必要条件
C．充要条件 D．既不充分也不必要条件
组卷：39引用：3难度：0.6
解析
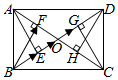5．2000多年前，古希腊雅典学派的第三大算学家欧道克萨斯首先提出黄金分割．所谓黄金分割，指的是把长为L的线段分为两部分，使其中一部分对于全部之比，等于另一部分对于该部分之比，黄金分割比为
5
-
1
2
≈0.618．其实有关“黄金分割”，我国也有记载，虽然没有古希腊的早，但它是我国古代数学家独立创造的．如图，在矩形ABCD中，AC，BD相交于点O，BF⊥AC，DH⊥AC，AE⊥BD，CG⊥BD，
BE
=
5
-
1
2
BO
，则
BF
=（　　）
A．
3
-
5
2
BA
+
5
+
5
10
BG
B．
3
-
5
2
BA
+
5
-
5
10
BG
C．
5
-
1
2
BA
+
5
-
5
10
BG
D．
3
-
5
2
BA
+
5
5
BG
组卷：82引用：5难度：0.6
解析
6．已知复数z满足z•
z
+4i
z
=5+ai,则实数a的取值范围为（　　）
A．[-4，4] B．[-6，6] C．[-8，8] D．[-12，12]
组卷：91引用：3难度：0.8
解析
7．已知点P是△ABC所在平面内一点，有下列四个等式：
甲：
PA
+
PB
+
PC
=
0
；乙：
PA
•
（
PA
-
PB
）
=
PC
•
（
PA
-
PB
）
；
丙：|
PA
|=|
PB
|=|
PC
|；丁：
PA
•
PB
=
PB
•
PC
=
PC
•
PA
．
如果只有一个等式不成立，则该等式为（　　）
A．甲 B．乙 C．丙 D．丁
组卷：606引用：11难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

21．治理垃圾是S市改善环境的重要举措．去年S市产生的垃圾量为200万吨，通过扩大宣传、环保处理等一系列措施，预计从今年开始，连续5年，每年的垃圾排放量比上一年减少20万吨，从第6年开始，每年的垃圾排放量为上一年的75%．
（1）写出S市从今年开始的年垃圾排放量与治理年数n（n∈N^*）的表达式；
（2）设A_n为从今年开始n年内的年平均垃圾排放量．如果年平均垃圾排放量呈逐年下降趋势，则认为现有的治理措施是有效的；否则，认为无效，试判断现有的治理措施是否有效，并说明理由．
组卷：127引用：5难度：0.6
解析
22．已知函数f（x）=ln（x+1）-1．
（1）求证：
f
（
x
-
1
）
≤
2
x
-
3
；
（2）设函数
g
（
x
）
=
（
x
+
1
）
f
（
x
）
-
1
2
a
x
2
+
1
，若g（x）在（0，+∞）上存在最大值，求实数a的取值范围．
组卷：120引用：5难度：0.2
解析

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A．必要不充分条件	B．充分不必要条件
C．充要条件	D．既不充分也不必要条件

A． 3 - 5 2 BA + 5 + 5 10 BG	B． 3 - 5 2 BA + 5 - 5 10 BG
C． 5 - 1 2 BA + 5 - 5 10 BG	D． 3 - 5 2 BA + 5 5 BG

2022-2023学年河北省衡水中学高三（上）第四次调研数学试卷

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．已知z=i（3-i）2+i，则z在复平面内对应的点位于（ ）

2．已知平面向量a，b满足|a|=2，b=（1，1），|a+b|=10，则a在b上的投影向量的坐标为（ ）

3．在直角三角形ABC中，A=90°，B=60°，AB=2，则AB•BC=（ ）

4．设A，B，C为平面内任意三点，则“AB与AC的夹角为钝角”是“|AB+AC|＜|BC|”的（ ）

6．已知复数z满足z•z+4iz=5+ai,则实数a的取值范围为（ ）

7．已知点P是△ABC所在平面内一点，有下列四个等式：甲：PA+PB+PC=0；乙：PA•（PA-PB）=PC•（PA-PB）；丙：|PA|=|PB|=|PC|；丁：PA•PB=PB•PC=PC•PA．如果只有一个等式不成立，则该等式为（ ）

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

22．已知函数f（x）=ln（x+1）-1．（1）求证：f（x-1）≤2x-3；（2）设函数g（x）=（x+1）f（x）-12ax2+1，若g（x）在（0，+∞）上存在最大值，求实数a的取值范围．

1．已知
z
=
i
（
3
-
i
）
2
+
i
，则z在复平面内对应的点位于（　　）

2．已知平面向量
a
，
b
满足
|
a
|
=
2
，
b
=
（
1
，
1
）
，
|
a
+
b
|
=
10
，则
a
在
b
上的投影向量的坐标为（　　）

3．在直角三角形ABC中，A=90°，B=60°，AB=2，则
AB
•
BC
=（　　）

4．设A，B，C为平面内任意三点，则“
AB
与
AC
的夹角为钝角”是“|
AB
+
AC
|＜|
BC
|”的（　　）

6．已知复数z满足z•
z
+4i
z
=5+ai,则实数a的取值范围为（　　）

7．已知点P是△ABC所在平面内一点，有下列四个等式：
甲：
PA
+
PB
+
PC
=
0
；乙：
PA
•
（
PA
-
PB
）
=
PC
•
（
PA
-
PB
）
；
丙：|
PA
|=|
PB
|=|
PC
|；丁：
PA
•
PB
=
PB
•
PC
=
PC
•
PA
．
如果只有一个等式不成立，则该等式为（　　）

22．已知函数f（x）=ln（x+1）-1．
（1）求证：
f
（
x
-
1
）
≤
2
x
-
3
；
（2）设函数
g
（
x
）
=
（
x
+
1
）
f
（
x
）
-
1
2
a
x
2
+
1
，若g（x）在（0，+∞）上存在最大值，求实数a的取值范围．