2022-2023学年吉林省通化市梅河口五中高一(下)期末数学试卷
发布:2024/6/26 8:0:9
一、单选题(本题共8小题,每题5分,共40分.在每小题列出的选项中,选出符合题目的一项)
-
1.已知圆锥轴截面为正三角形,母线长为2,则该圆锥的体积等于( )
组卷:437引用:9难度:0.9 -
2.若
,P(AB)=19,P(A)=23,则事件A与B的关系是( )P(B)=13组卷:808引用:14难度:0.8 -
3.在下列判断两个平面α与β平行的4个命题中,真命题的个数是( )
(1)α、β都垂直于平面r,那么α∥β.
(2)α、β都平行于平面r,那么α∥β.
(3)α、β都垂直于直线l,那么α∥β.
(4)如果l、m是两条异面直线,且l∥α,m∥α,l∥β,m∥β,那么α∥β.组卷:234引用:7难度:0.8 -
4.甲、乙两校各有3名教师报名支教,其中甲校2男1女,乙校1男2女,若从甲校和乙校报名的教师中各任选1名,则选出的2名教师性别相同的概率是( )
组卷:246引用:9难度:0.7 -
5.已知向量
,a=(5,12),b=(2,0),若c=a+tb,则t=( )〈a,c〉=〈b,c〉组卷:63引用:3难度:0.8 -
6.如图1,在高为h的直三棱柱容器ABC-A1B1C1中,现往该容器内灌进一些水,水深为2,然后固定容器底面的一边AB于地面上,再将容器倾斜,当倾斜到某一位置时,水面恰好为A1B1C(如图2),则容器的高h为( )
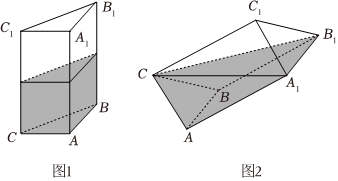 组卷:184引用:7难度:0.7
组卷:184引用:7难度:0.7 -
7.在正四棱锥P-ABCD中,PA=AB=2,M为棱PC的中点,则异面直线AC,BM所成角的余弦值为( )
组卷:178引用:4难度:0.7
四、解答题(本题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤)
-
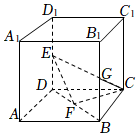 21.如图,在棱长为1的正方体ABCD-A1B1CD1中,E,F,G分别是DD1,BD,BB1的中点.
21.如图,在棱长为1的正方体ABCD-A1B1CD1中,E,F,G分别是DD1,BD,BB1的中点.
(1)求EF与CG所成角的余弦值;
(2)求点G到平面CEF的距离.组卷:118引用:7难度:0.6 -
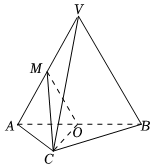 22.三棱锥V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且,O、M分别为AB、VA的中点.AC=BC=2
22.三棱锥V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且,O、M分别为AB、VA的中点.AC=BC=2
(1)求证:VB∥平面MOC;
(2)求证:平面MOC⊥平面VAB;
(3)求三棱锥V-ABC的体积.
(要求此题使用定理证明)组卷:210引用:5难度:0.7


