当前位置：试卷中心 > 试卷详情

2022-2023学年湖南省永州市零陵区七年级（下）期末数学试卷

发布：2024/7/1 8:0:9

一、选择题（本大题共10个小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的；请将你认为正确的选项填涂到答题卡上）

1．下列图形中，轴对称图形的个数是（　　）
A．1个 B．2个 C．3个 D．4个
组卷：84引用：3难度：0.9
解析
2．下列运算正确的是（　　）
A．a³+a⁴=a⁷ B．2x-x=2 C．5m²•m³=5m⁵ D．（-3m）²=6m²
组卷：34引用：2难度：0.7
解析
3．如图，如果∠1=∠2．那么a∥b,其依据可以简单的说成（　　）
A．两直线平行，内错角相等
B．两直线平行，同位角相等
C．同位角相等，两直线平行
D．内错角相等，两直线平行
组卷：56引用：2难度：0.8
解析
4．下列计算中，正确的是（　　）
A．（a-b）²=a²-b²
B．-x（3x²-1）=-3x³-x
C．（a+b）（a-b）=a²+b²
D．（m+n）（m-2n）=m²-mn-2n²
组卷：19引用：3难度：0.6
解析
5．计算：
（
-
1
2
）
2022
•
2
2023
的结果是（　　）
A．-1 B．1 C．-2 D．2
组卷：291引用：7难度：0.7
解析
6．已知一组数据-1，4，x,6，15的众数为6，那么这组数据的中位数是（　　）
A．-1 B．4 C．5 D．6
组卷：40引用：3难度：0.5
解析
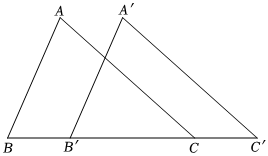7．如图，将三角形ABC沿着射线BC方向平移得到三角形A′B′C′，已知AA′之间的距离是1，B′C=2，则B′C′的长为（　　）
A．2 B．3 C．4 D．5
组卷：65引用：4难度：0.5
解析
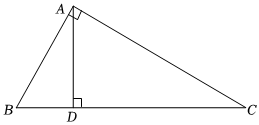8．如图，AB⊥AC，AD⊥BC，垂足分别为A，D，已知AB=3，AC=4，BC=5，则图中点A到BC的距离是（　　）
A．5 B．4 C．3 D．
12
5
组卷：109引用：5难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本大题共9个小题，共72分，解答题要求写出必要的文字说明或解答过程）

24．配方法是数学中重要的思想方法之一，它是指将一个式子的某一部分通过恒等变形化为一个完全平方式或几个完全平方式的和的方法，这种方法常被用到代数式的变形中，并结合非负数的意义来解决一些问题．我们定义：一个整数能表示成a²+b²（a,b是整数）的形式，则称这个数为“完美数”，例如，5是“完美数”．理由：因为5=2²+1²，所以5是“完美数”．
【解决问题】
（1）已知13是“完美数”，请将它写成a²+b²（a,b是正整数）的形式
；
（2）若x²-4x+53可配方成（x-m）²+n²（m,n为正整数），则m+n=
；
【探究问题】
（3）已知S=x²+9y²+8x-12y+k（x,y是整数，k是常数），要使S为“完美数”，试求出符合条件的一个k值，并说明理由．
组卷：255引用：4难度：0.5
解析
25．如图所示，将一副三角板中的两块直角三角板按图1放置，∠BAC=∠BCA=45°，∠EDF=60°，∠DFE=30°，∠ABC=∠DEF=90°，此时点A与点D重合，点A，C，E三点共线．

（1）对于图1，固定三角形DEF的位置不变，将三角形ABC绕点A按顺时针方向进行旋转，旋转至AB与DF首次垂直，如图2所示，此时∠CAE的度数是
；
（2）若直线MN∥PQ，固定三角形DEF的位置不变，将图1中的三角形ABC沿DE方向平移，使得点C正好落在直线MN上，再将三角形ABC绕点C按逆时针方向进行旋转，如图3所示．
①若边AC与边EF相交于点G，试判断∠CGF-∠ACM的值是否为定值，若是定值，则求出该定值；若不是定值，请说明理由；
②固定三角形DEF的位置不变，将三角形ABC绕点C按逆时针方向以每秒15°的速度旋转，至AC与直线MN首次重合时停止运动．设旋转时间为t.
问：当t为何值时，线段AB与三角形DEF的一条边平行（选择你喜欢的一条边探究，如果符合条件的t不存在，只要理由充分，也可得分）．
组卷：118引用：1难度：0.3
解析