2022-2023学年安徽省亳州市第二完全中学高二（下）期末数学试卷（A卷）

一、单选题

• 1．若集合A={x|x²-5x-6≤0}，B={x|x＞7}，则（∁_RA）∩B=（　　）

  A．（-1，7]

  B．（-1，6]

  C．（7，+∞）

  D．（6，+∞）
  组卷：221引用：4难度：0.9

  解析

• 2．设x,y∈R，则“x=-y”是“x²-y²-x-y=0”的（　　）

  A．充分必要条件	B．充分不必要条件
  C．必要不充分条件	D．既不充分也不必要条件
  组卷：139引用：3难度：0.9

  解析

• 3．已知定义域为R的函数f（x）在[1，+∞）上单调递减，且f（x+1）是偶函数，不等式f（3m+1）≥f（x-2）对任意的x∈[-1，0]恒成立，则实数m的取值范围是（　　）

  A． [ - 1 2 ， 1 2 ]

  B．[-1，1]

  C． [ 0 ， 1 2 ]

  D．[-1，0]
  组卷：318引用：3难度：0.5

  解析

• 4．某单位制作了一个热气球用于广告宣传．已知热气球在第一分钟内能上升30米，以后每分钟上升的高度都是前一分钟的

  2

  3

  ，则该气球上升到70米至少要经过（　　）

  A．3分钟

  B．4分钟

  C．5分钟

  D．6分钟
  组卷：21引用：3难度：0.7

  解析

• 5．已知奇函数f（x）满足f′（-1）=1，则

  lim

  Δ

  x

  →

  0

  f

  （

  Δ

  x

  -

  1

  ）

  +

  f

  （

  1

  ）

  2

  Δ

  x

  =（　　）

  A．- 1 2

  B． 1 2

  C．1

  D．-1
  组卷：183引用：3难度：0.9

  解析

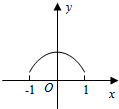• 6．已知函数y=f（x）的图象是下列四个图象之一，且其导函数y=f′（x）的图象如图所示，则该函数的图象是（　　）

  A．

  B．

  C．

  D．
  组卷：1885引用：98难度：0.9

  解析

• 7．已知数列{a_n}满足a₁+3a₂+…+（2n-1）a_n=2n,则数列

  {

  a

  n

  2

  n

  +

  1

  }

  的前10项和是（　　）

  A． 10 21

  B． 11 23

  C． 20 21

  D． 22 23
  组卷：415引用：7难度：0.5

  解析

四、解答题

• 21．已知数列{a_n}中，a₁=1，a_n+1=3a_n+1．
  （Ⅰ）求证：

  {

  a

  n

  +

  1

  2

  }

  是等比数列，并求{a_n}的通项公式；
  （Ⅱ）数列{b_n}满足b_n=（3ⁿ-1）•

  n

  2

  n

  +

  1

  •

  a

  n

  ，数列{b_n}的前n项和为T_n，若不等式（-1）ⁿλ＜T_n+

  n

  2

  n

  对一切n∈N^*恒成立，求λ的取值范围．
  组卷：248引用：3难度：0.5

  解析

• 22．已知函数f（x）=axlnx-

  1

  2

  x

  2

  -ax.
  （1）讨论函数f（x）的导函数的单调性；
  （2）若对∀x₁，x₂∈（1，e），都有

  f

  （

  x

  1

  ）

  -

  f

  （

  x

  2

  ）

  x

  1

  -

  x

  2

  ＜

  3

  ，求a的取值范围．
  组卷：168引用：6难度：0.4

  解析