2022-2023学年浙江省宁波市余姚市兰江中学九年级（上）第二次质检数学试卷

一、单选题（共10小题，每小题4分，共40分）

• 1．已知抛物线y=2（x-3）²-5，其对称轴是（　　）

  A．直线x=-3

  B．直线x=3

  C．直线x=-5

  D．直线x=5
  组卷：166引用：5难度：0.8

  解析

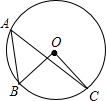• 2．如图，点A，B，C在⊙O上，∠A=50°，则∠BOC的度数为（　　）

  A．40°

  B．50°

  C．80°

  D．100°
  组卷：888引用：90难度：0.9

  解析

• 3．下列事件中，属于必然事件的是（　　）

  A．三个点确定一个圆

  B．每条边都相等的多边形是正多边形

  C．平分弦的直径垂直于弦

  D．直径所对的圆周角是直角
  组卷：59引用：5难度：0.8

  解析

• 4．浙江省积极响应国家“节约资源，保护环境”的号召，利用自身地域环境优势，加强可再生资源——风能的利用，其中，海上风电产业具有技术先导性强、经济体量大和产业关联度大的特点，如图是海上风力发电装置，转子叶片图案绕中心旋转n°后能与原图案重合，则n可以取（　　）

  A．60

  B．90

  C．120

  D．180
  组卷：221引用：5难度：0.8

  解析

• 5．已知函数y=-x²+bx+c,其中b＞0，c＜0，此函数的图象可以是（　　）

  A．

  B．

  C．

  D．
  组卷：404引用：8难度：0.7

  解析

• 6．二次函数y=mx²-4x+1有最小值-3，则m等于（　　）

  A．1

  B．-1

  C．±1

  D．± 1 2
  组卷：677引用：13难度：0.9

  解析

• 7．如图，四边形ABCD是⊙O的内接四边形，若∠D=3∠B，则∠B的度数为（　　）

  A．30°

  B．36°

  C．45°

  D．60°
  组卷：435引用：7难度：0.8

  解析

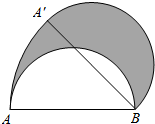• 8．如图，AB为半圆的直径，且AB=4，半圆绕点B顺时针旋转45°，点A旋转到A′的位置，则图中阴影部分的面积为（　　）

  A．π

  B．2π

  C． π 2

  D．4π
  组卷：1224引用：8难度：0.7

  解析

三、解答题（第17-19题各8分，第20-22题各10分，第23题12分，第24题14分，共80分）

• 23．如图，二次函数y=x²+bx+c的图象交x轴于点A（-3，0），B（1，0），交y轴于点 C．点P（m,0）是x轴上的一动点，PM⊥x轴，交直线AC于点M，交抛物线于点N．
  （1）求这个二次函数的表达式；
  （2）①若点P仅在线段AO上运动，如图，求线段MN的最大值；
  ②若点P在x轴上运动，则在y轴上是否存在点Q，使以M，N，C，Q为顶点的四边形为菱形．若存在，请直接写出所有满足条件的点Q的坐标；若不存在，请说明理由．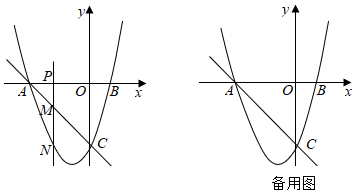
  
  组卷：8995引用：28难度：0.1

  解析

• 24．如图，在△ABC中，D在边AC上，圆O为锐角△BCD的外接圆，连结CO并延长交AB于点E．
  （1）若∠DBC=α，请用含α的代数式表示∠DCE；
  （2）如图2，作BF⊥AC，垂足为F，BF与CE交于点G，已知∠ABD=∠CBF．
  ①求证：EB=EG；
  ②若CE=5，AC=8，求FG+FB的值．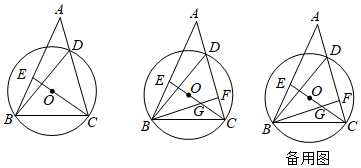
  
  组卷：3241引用：10难度：0.1

  解析