2023-2024学年浙江省杭州市拱墅区文澜中学九年级（上）月考数学试卷（10月份）

一、仔细选一选（本题有10个小题，每小题3分，共30分）下面每小题给出四个选项中，只有一个是正确的．注意可以用多种不同的方法来选取正确的答案．

• 1．已知⊙O的半径为5，PO=4，则点P在（　　）

  A．圆内

  B．圆上

  C．圆外

  D．不确定
  组卷：136引用：5难度：0.7

  解析

• 2．抛物线y=x²+2x+3与x轴的交点的个数有（　　）

  A．0个

  B．1个

  C．2个

  D．3个
  组卷：95引用：9难度：0.7

  解析

• 3．已知点A，B，且AB＜4，画经过A，B两点且半径为2的圆有（　　）

  A．0个

  B．1个

  C．2个

  D．无数个
  组卷：423引用：3难度：0.7

  解析

• 4．对于抛物线y=-2（x+1）²-3，下列结论：①抛物线的开口向下：②对称轴为直线x=1；③顶点坐标为（-1，3）；④有最小值为-3，其中正确结论的个数为（　　）

  A．1

  B．2

  C．3

  D．4
  组卷：171引用：2难度：0.5

  解析

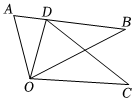• 5．如图，△ODC是由△OAB绕点O顺时针旋转32°后得到的图形，若点D恰好落在AB上，且∠AOC的度数为100°，则∠DOB的度数是（　　）

  A．32°

  B．36°

  C．38°

  D．40°
  组卷：398引用：5难度：0.6

  解析

• 6．已知三点（2，a），（-1，b），（3，c）在抛物线y=x²+x+2上，则a,b,c的大小关系是（　　）

  A．c＞a＞b	B．b＞a＞c
  C．a＞b＞c	D．无法比较大小
  组卷：162引用：3难度：0.5

  解析

• 7．正六边形内接于圆，它的边所对的圆周角是（　　）

  A．60°

  B．120°

  C．60°或120°

  D．30°或150°
  组卷：1204引用：9难度：0.9

  解析

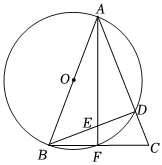• 8．如图，在△ABC中，以AB为直径的⊙O分别与BC，AC交于点F，D，点F是

  ˆ

  BD

  的中点，连接AF，BD交于点E．若AB=10，CD=4．连接DF，则弦DF的长为（　　）

  A． 2 5

  B． 4 5

  C．4

  D．5
  组卷：992引用：9难度：0.6

  解析

三、全面答一答（本题有8个小题，共66分）解答应写出文字说明，证明过程或演算步骤．如果觉得有的题目有点困难，那么把自己能写出的解答写出一部分也可以．

• 23．如图1，C，D是半圆ACB上的两点，若直径AB上存在一点P，满足∠APC=∠BPD，则称∠CPD是

  ˆ

  CD

  的“幸运角”．
  （1）如图2，AB是⊙O的直径，弦CE⊥AB，D是BC上一点，连结ED交AB于点P，连结CP，∠CPD是

  ˆ

  CD

  的“幸运角”吗？请说明理由；
  （2）设

  ˆ

  CD

  的度数为n,请用含n的式子表示

  ˆ

  CD

  的“幸运角”度数；
  （3）在（1）的条件下，直径AB=10，

  ˆ

  CD

  的“幸运角”为90°．
  ①如图3，连结CD，求弦CD的长；
  ②当

  DE

  =

  7

  2

  时，求CE的长．
  
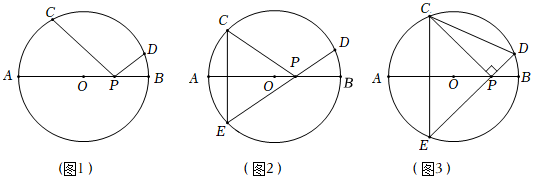  组卷：653引用：3难度：0.3

  解析

• 24．已知抛物线y=ax²+bx+c的顶点为（3，2），且过点（0，11）．
  （Ⅰ）求抛物线的解析式；
  （Ⅱ）将抛物线先向左平移2个单位长度，再向下平移m（m＞0）个单位长度后得到新抛物线．
  ①若新抛物线与x轴交于A，B两点（点A在点B的左侧），且OB=3OA，求m的值；
  ②若P（x₁，y₁），Q（x₂，y₂）是新抛物线上的两点，当n≤x₁≤n+1，x₂≥4时，均有y₁≤y₂，求n的取值范围．
  组卷：1774引用：8难度：0.4

  解析