2022-2023学年北京二中高二（下）期末物理试卷

一、单项选择题（本题共10小题，每小题3分，共30分）

• 1．2020年12月4日，新一代“人造太阳”装置--中国环流器二号M装置（HL-2M）在成都建成并首次实现利用核聚变放电。下列方程中，正确的核聚变反应方程是（　　）

  A． 2 1 H+ 3 1 H→ 4 2 He+ 1 0 n

  B． 238 92 U→ 234 90 Th+ 4 2 He

  C． 235 92 U+ 1 0 n→ 144 56 Ba+ 89 36 Kr+3 1 0 n

  D． 4 2 He+ 27 13 Al→ 30 15 P+2 1 0 n
  组卷：523引用：10难度：0.8

  解析

• 2．如图所示的α粒子散射实验中，少数α粒子发生大角度偏转的原因是（　　）

  A．α粒子与原子中的电子发生碰撞

  B．正电荷在原子中均匀分布

  C．原子中带正电的部分和绝大部分质量集中在一个很小的核上

  D．原子只能处于一系列不连续的能量状态中
  组卷：262引用：3难度：0.7

  解析

• 3．下列说法正确的是（　　）
  

  A．甲图中的酱油蛋是布朗运动的结果

  B．乙图中的水黾可以停在水面，是因为水具有表面张力

  C．丙图中酱油与左边材料不浸润，与右边材料浸润

  D．丁图中电冰箱能把热量从低温的箱内传到高温的箱外，违背了热力学第二定律
  组卷：59引用：2难度：0.6

  解析

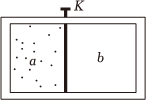• 4．如图，一绝热容器被隔板K隔开成a,b两部分．已知a内有一定量的稀薄气体，b内为真空．抽开隔板K后，a内气体进入b,最终达到平衡状态．在此过程中（　　）

  A．气体对外界做功，内能减少

  B．外界对气体做功，内能增加

  C．气体压强变小，温度降低

  D．气体压强变小，温度不变
  组卷：188引用：2难度：0.7

  解析

• 5．一列简谐横波沿x轴正方向传播，在t=0时的波形如图甲所示，L、M、N是波上的三个质点，图乙是其中一个质点在此后一段时间内的振动图像。下列说法正确的是（　　）
  

  A．t=0时，质点M沿y轴正方向运动

  B．t=0时，质点M的加速度比质点N的小

  C．图乙是质点N的振动图像

  D．质点L和质点N的相位总是相同
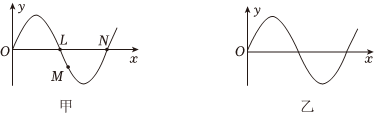  组卷：200引用：2难度：0.6

  解析

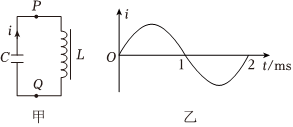• 6．如图甲所示的LC振荡电路中，通过P点的电流随时间变化的图线如图乙所示，若把通过P点向右规定为电流的正方向，则（　　）

  A．1～1.5ms内，Q点比P点电势低

  B．1～1.5ms内，电场能正在增加

  C．0.5～1ms内，电容器C正在放电

  D．0.5～1ms内，电容器的上极板带负电荷
  组卷：170引用：6难度：0.8

  解析

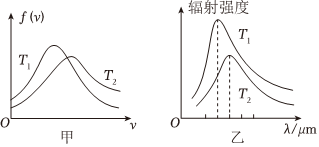• 7．某气体在T₁、T₂两种不同温度下的分子速率分布图象如图甲所示，纵坐标f（v）表示各速率区间的分子数占总分子数的百分比，横坐标v表示分子的速率；而黑体辐射的实验规律如图乙所示，图乙中画出了T₁、T₂两种不同温度下黑体辐射的强度与波长的关系。下列说法正确的是（　　）

  A．图甲中T1＞T2

  B．图乙中T1＜T2

  C．图甲中温度升高，所有分子的速率都增大

  D．图乙中温度升高，辐射强度的极大值向波长较短方向移动
  组卷：462引用：3难度：0.7

  解析

四、计算题（本题共4小题，共43分）

• 21．激光由于其单色性好、亮度高、方向性好等特点，在科技前沿的许多领域有着广泛的应用。光子的能量E、动量p以及光在真空中的传播速度为c满足关系：E=pc。
  （1）科研人员曾用强激光做过一个有趣的实验：一个水平放置的小玻璃片被一束强激光托在空中。已知激光竖直向上照射到质量为m的小玻璃片上后，全部被小玻璃片吸收，重力加速度为g,光在真空中的传播速度为c。求激光照射到小玻璃片上的功率P₀；
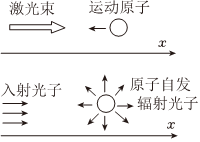
  （2）激光冷却和原子捕获技术在科学上意义重大，特别是对生物科学将产生重大影响。所谓激光冷却就是在激光的作用下使得做热运动的原子减速，其具体过程如下：一质量为m的原子沿着x轴负方向运动，波长为λ₀的激光束迎面射向该原子。运动着的原子就会吸收迎面而来的光子从基态跃迁，而处于激发态的原子会立即自发地辐射光子回到基态。在回到基态过程中，原子向各方向辐射光子的可能性可认为是均等的，因而辐射不再对原子产生合外力的作用效果，并且可认为原子的质量没有变化。已知普朗克常量为h,光在真空中的传播速度为c。
  ①设原子单位时间内与n个光子发生相互作用，求运动原子做减速运动的加速度a的大小；
  ②假设该基态原子以速度v₀沿着x轴负方向运动，当该原子吸收一个波长为λ₀的光子的能量后跃迁到了第一激发态，且原子的速度大小发生了变化，但方向未变，请列出求该原子的第一激发态与其基态的能级差ΔE的力学方程（或方程组）。（只列方程不求解，且不需考虑相对论效应）
  组卷：116引用：1难度：0.3

  解析

• 22．简谐振动是物理学中很重要的一种运动形式，不同的简谐振动现象各异，但却遵循着相似的规律。例如，一个质量为m,劲度系数为k的弹簧振子，其位移x随时间t按正余弦规律做周期性变化，周期公式是：T=2π

  m

  k

  ，同时在振子周期性运动的过程中其动能和能相互转化，但总能量保持不变，即：

  1

  2

  m

  v

  2

  +

  1

  2

  k

  x

  2

  =E，其中E为系统的总能量，v=

  Δ

  x

  Δ

  t

  为振子位移为x时的瞬时速度。
  结合简谐振动的上述知识，通过类比的方法分析下面几个问题。
  （1）如图1所示，在LC振荡电路中，电容器极板上的带电量q与电路中的电流i=

  Δ

  q

  Δ

  t

  随时间t都是按正余弦规律做周期性变化的。同时线圈储存的磁场能和电容器储存的电场能相互转化，但总能量E保持不变，即：

  1

  2

  L

  i

  2

  +

  1

  2

  •

  q

  2

  C

  =E。其中L为线圈的自感系数，C为电容器的电容。类比弹簧振子中的各物理量，电容器极板上的带电量q相当于弹簧振子中的哪个物理量？并类比简谐振动公式写出LC振荡的周期公式；
  （2）如图2所示，摆长为L，小球质量为m的单摆，当最大偏角较小时，摆动过程中其摆角随时间也是按正余弦规律变化的。写出单摆摆角为θ、小球角速度为ω时系统总能量的表达式，并类比弹簧振子的规律求出单摆摆动的周期；（已知θ很小时，cosθ≈1-

  1

  2

  θ

  2

  ）
  （3）如图3所示，长为L的轻杆（质量不计），一端可绕固定在O点的光滑轴承在竖直平面内转动，在距点为

  L

  2

  和L处分别固定一个质量为m、可看作质点的小球。类比弹簧振子的规律求出系统在竖直平面内做小角度摆动时的周期。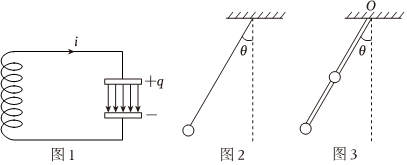
  
  组卷：153引用：1难度：0.2

  解析