简谐振动是物理学中很重要的一种运动形式，不同的简谐振动现象各异，但却遵循着相似的规律。例如，一个质量为m,劲度系数为k的弹簧振子，其位移x随时间t按正余弦规律做周期性变化，周期公式是：T=2π

m

k

，同时在振子周期性运动的过程中其动能和能相互转化，但总能量保持不变，即：

1

2

m

v

2

+

1

2

k

x

2

=E，其中E为系统的总能量，v=

Δ

x

Δ

t

为振子位移为x时的瞬时速度。
结合简谐振动的上述知识，通过类比的方法分析下面几个问题。
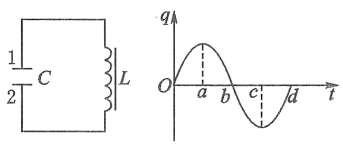
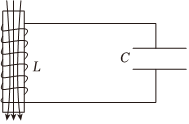
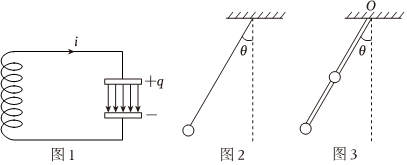
（1）如图1所示，在LC振荡电路中，电容器极板上的带电量q与电路中的电流i=

Δ

q

Δ

t

随时间t都是按正余弦规律做周期性变化的。同时线圈储存的磁场能和电容器储存的电场能相互转化，但总能量E保持不变，即：

1

2

L

i

2

+

1

2

•

q

2

C

=E。其中L为线圈的自感系数，C为电容器的电容。类比弹簧振子中的各物理量，电容器极板上的带电量q相当于弹簧振子中的哪个物理量？并类比简谐振动公式写出LC振荡的周期公式；
（2）如图2所示，摆长为L，小球质量为m的单摆，当最大偏角较小时，摆动过程中其摆角随时间也是按正余弦规律变化的。写出单摆摆角为θ、小球角速度为ω时系统总能量的表达式，并类比弹簧振子的规律求出单摆摆动的周期；（已知θ很小时，cosθ≈1-

1

2

θ

2

）
（3）如图3所示，长为L的轻杆（质量不计），一端可绕固定在O点的光滑轴承在竖直平面内转动，在距点为

L

2

和L处分别固定一个质量为m、可看作质点的小球。类比弹簧振子的规律求出系统在竖直平面内做小角度摆动时的周期。