当前位置：试卷中心 > 试卷详情

2022-2023学年北京市海淀区师达中学九年级（下）大练习数学试卷（4月份）

发布：2024/5/8 8:0:8

一、选择题（共16分，每题2分）

1．如图是某几何体的三视图，该几何体是（　　）
A．三棱柱 B．长方体 C．圆锥 D．圆柱
组卷：106引用：6难度：0.7
解析
2．2021年我国加大农村义务教育薄弱环节建设力度，提高学生营养改善计划补助标准，约37000000学生受益．将37000000用科学记数法表示应为（　　）
A．0.37×10⁶ B．3.7×10⁶ C．3.7×10⁷ D．37×10⁶
组卷：33引用：5难度：0.7
解析
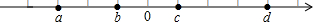3．实数a,b,c,d在数轴上对应的点的位置如图所示，下列结论正确的是（　　）
A．|a|＜|b| B．ad＞0 C．a+c＞0 D．d-a＞0
组卷：277引用：11难度：0.8
解析
4．若一个多边形的每个外角都是30°，则这个多边形的边数为（　　）
A．6 B．8 C．10 D．12
组卷：611引用：22难度：0.7
解析
5．在一个不透明的袋子中，有1个白球和2个红球，它们只有颜色上的区别，从袋子中随机地摸出一个球记下颜色放回．再随机地摸出一个球．则两次都摸到白球的概率为（　　）
A．
1
9
B．
1
6
C．
1
3
D．
1
2
组卷：50引用：4难度：0.7
解析
6．如图，直线a∥b,点B在直线a上，AB⊥BC，若∠1=40°，则∠2的度数为（　　）
A．40° B．50° C．80° D．140°
组卷：328引用：9难度：0.7
解析
7．A（-
1
2
，y₁），B（1，y₂），C（4，y₃）三点都在二次函数y=-（x-2）²+k的图象上，则y₁，y₂，y₃的大小关系为（　　）
A．y₁＜y₂＜y₃ B．y₁＜y₃＜y₂ C．y₃＜y₁＜y₂ D．y₃＜y₂＜y₁
组卷：2250引用：28难度：0.4
解析
8．如图1，点P从△ABC的顶点B出发，沿B→C→A匀速运动到点A，图2是点P运动时，线段BP的长度随时间x变化的关系图象，其中M是曲线部分的最低点，则△ABC的面积是（　　）
A．30 B．60 C．78 D．156
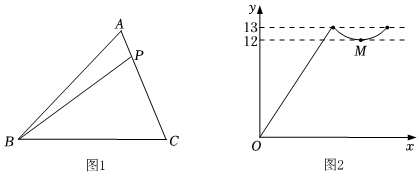组卷：704引用：4难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（共60分，第17-18题，每题5分，第19-24题6分，第25-26题，每题7分）

25．在平面直角坐标系xOy中，抛物线y=ax²+bx+3a（a≠0）与x轴的交点为点A（1，0）和点B．
（1）用含a的式子表示b；
（2）求抛物线的对称轴和点B的坐标；
（3）分别过点P（t,0）和点Q（t+2，0）作x轴的垂线，交抛物线于点M和点N，记抛物线在M，N之间的部分为图象G（包括M，N两点）．记图形G上任意一点的纵坐标的最大值是m,最小值为n.
①当a=1时，求m-n的最小值；
②若存在实数t,使得m-n=1，直接写出a的取值范围．
组卷：1081引用：3难度：0.1
解析
26．在Rt△ABC中，∠ABC=90°，∠BAC=30°，D为边BC延长线上一动点，点E在边AC延长线上，CE=CD．点D关于点B的对称点为点F，连接AD，EF．
（1）设CD=a,BC=b.判断AE与CF的数量关系，并证明；
（2）取AD中点P，连接PE、PF，补全图形，判断PE与PF的数量关系与位置关系，并证明．
组卷：219引用：2难度：0.5
解析