2022-2023学年广东省深圳市罗湖区八年级（下）期末数学试卷

一、选择题（本题共10小题，每题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的）

• 1．“二十四节气”是中华上古农耕文明的智慧结晶．下列四幅标识图，其中文字上面图案是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：412引用：13难度：0.9

  解析

• 2．下列等式，从左到右的变形是因式分解的是（　　）

  A．x（x-2）=x2-2x	B．6x2y=6x•xy
  C．x2-4=（x+2）（x-2）	D． x + 2 = x （ 1 + 2 x ）
  组卷：514引用：3难度：0.8

  解析

• 3．将分式

  x

  x

  +

  y

  中的x,y的值同时扩大2倍，则分式的值（　　）

  A．扩大2倍	B．缩小到原来的 1 2
  C．保持不变	D．无法确定
  组卷：486引用：3难度：0.8

  解析

• 4．交通法规人人遵守，文明城市处处安全．在通过桥洞时，我们往往会看到如图所示的标志，这是限制车高的标志，则通过该桥洞的车高x（m）的范围可表示为（　　）

  A．x≥4.5

  B．x＞4.5

  C．x≤4.5

  D．0＜x≤4.5
  组卷：2217引用：22难度：0.9

  解析

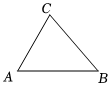• 5．三条公路将A、B、C三个村庄连成一个如图的三角形区域，如果在这个区域内修建一个集贸市场，要使集贸市场到三条公路的距离相等，那么这个集贸市场应建的位置是（　　）

  A．三条高线的交点	B．三条中线的交点
  C．三条角平分线的交点	D．三边垂直平分线的交点
  组卷：11013引用：89难度：0.9

  解析

• 6．直线l₁：y₁=k₁x与直线l₂：y₂=k₂x+b在同一平面直角坐标系中的位置关系如图所示，则关于x的不等式k₁x＞k₂x+b的解集为（　　）

  A．x＞2

  B．x＜2

  C．x＞3

  D．x＜3
  组卷：527引用：5难度：0.9

  解析

• 7．在课堂上，陈老师发给每人一张印有Rt△ABC（如图1）的卡片，然后要求同学们画一个Rt△A'B'C'，使得Rt△A'B'C'≌Rt△ABC．小赵和小刘同学先画出了∠MB'N=90°之后，后续画图的主要过程分别如图所示．
  
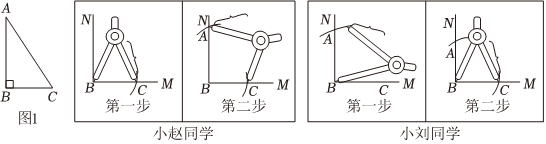
  对这两种画法的描述中正确的是（　　）

  A．小赵同学作图判定Rt△A'B'C'≌Rt△ABC的依据是HL

  B．小赵同学第二步作图时，用圆规截取的长度是线段BC的长

  C．小刘同学作图判定Rt△A'B'C'≌Rt△ABC的依据是ASA

  D．小刘同学第一步作图时，用圆规截取的长度是线段AC的长
  组卷：366引用：5难度：0.5

  解析

三、解答题（共7小题，共55分，其中16题8分，17题6分，18题6分，19题8分，20题8分，21题9分，22题10分）

• 21．【阅读理解】我们在分析解决某些数学问题时，经常要比较两个数或代数式的大小，解决此类问题时一般要进行转化，其中“作差法”就是常用的方法之一．其依据是不等式（或等式）的性质：若x-y＞0，则x＞y；若x-y=0，则x=y；若x-y＜0，则x＜y.
  例：已知M=a²-ab,N=ab-b²，其中a≠b,求证：M＞N．
  证明：M-N=a²-ab-ab+b²=（a-b）²，
  ∵a≠b,
  ∴（a-b）²＞0，故M＞N，
  【新知理解】
  （1）比较大小：x-3

  2+x.（填“＞”，“=”，“＜”）
  【问题解决】
  （2）甲、乙两个平行四边形，其底和高如图所示（a为正整数），其面积分别为S₁，S₂．请比较S₁，S₂的大小关系．
  
  【拓展应用】
  （3）请用“作差法”解决下列问题：
  某游泳馆在暑假期间对学生优惠开放，有A，B两种方案可供选择，A方案：每次按原价打9折收费；B方案：前5次按照原价收费，从第6次起每次打8折．请问游泳的学生选择哪种方案更合算？
  组卷：1123引用：7难度：0.5

  解析

• 22．【探究发现】
  （1）如图1，在△ABC中，AB=AC．AH⊥BC，垂足为H，点D在AH上，连接BD，CD，则有下列命题：①△ABD≌△ACD；②△BDH≌△CDH．
  请你从中选择一个命题证明其真假，并写出证明过程．
  【类比迁移】
  （2）如图2，在△ABC中，AB=AC，∠BAC=45°，点D在三角形的内部，过点D作BD⊥CD，且BD=CD，连接AD．求证：AD=BD=CD．
  【拓展提升】
  （3）如图3，在△ABC中，∠BAC=45°，BC=5，把线段AB绕点A顺时针方向旋转90°到AM，把线段AC绕点A逆时针旋转90°到AN，分别连接MB，NC，MN，请直接写出△AMN面积的最大值．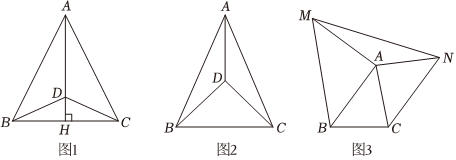
  
  组卷：1197引用：2难度：0.1

  解析