当前位置：试卷中心 > 试卷详情

2023-2024学年福建省泉州市南安市华侨中学高二（上）月考数学试卷（8月份）

发布：2024/8/16 17:0:1

一、单选题

1．如图，在三棱锥P-ABC中，E，F，G，H，I，J分别为线段PA，PB，PC，AB，BC，CA的中点，则下列说法正确的是（　　）
A．PH∥BG B．IE∥CP C．FH∥GJ D．GI∥JH
组卷：302引用：4难度：0.7
解析
2．已知
a
、
b
是不共线的向量，
AB
=
λ
a
+
b
，
AC
=
a
+
μ
b
（λ、μ∈R），当且仅当（　　）时，A、B、C三点共线．
A．λ+μ=1 B．λ-μ=1 C．λμ=-1 D．λμ=1
组卷：287引用：5难度：0.9
解析
3．设m,n是空间两条不同的直线，α，β是空间两个不同的平面．给出下列四个命题：
①若m∥α，n∥β，α∥β，则m∥n；
②若α⊥β，m⊥β，m⊄α，则m∥α；
③若m⊥n,m⊥α，α∥β，则n∥β；
④若α⊥β，α∩β=l,m∥α，m⊥l,则m⊥β．
其中正确的是（　　）
A．①② B．②③ C．② D．②④
组卷：35引用：1难度：0.7
解析
4．在正四面体ABCD中，点E，F，G分别为棱BC，CD，AC的中点，则异面直线AE，FG所成角的余弦值为（　　）
A．
1
2
B．
3
5
C．
3
3
D．
6
3
组卷：559引用：9难度：0.7
解析
5．如图，已知点O是边长为1的等边△ABC的中心，则（
OA
+
OB
）•（
OA
+
OC
）等于（　　）
A．
1
9
B．
-
1
9
C．
1
6
D．
-
1
6
组卷：55引用：21难度：0.9
解析
6．已知长方体ABCD-A₁B₁C₁D₁中，AB=4，BC=2，点P为BB₁中点，设平面A₁PC₁∩BC=F，平面A₁PC₁∩AB=E，则线段EF长度为（　　）
A．
3
B．
5
C．
2
5
D．5
组卷：10引用：1难度：0.7
解析
7．在三棱锥S-ABC中，SA=SB=
2
，AB=2，BC=1，AB⊥BC，若SC与面SAB所成角的最大值为θ，则tan²θ的值为（　　）
A．
1
2
B．
2
2
C．
5
-
1
2
D．
5
+
1
2
组卷：632引用：5难度：0.2
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题

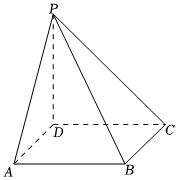21．如图，四棱锥P-ABCD的底面为正方形，PD⊥底面ABCD．设平面PAD与平面PBC的交线为l.
（1）证明：l⊥平面PDC；
（2）已知PD=AD=1，Q为l上的点且，
DA
=
m
PQ
（m＞0），求PB与平面QCD所成角的正弦值的最大值．
组卷：97引用：1难度：0.5
解析
22．如图，四边形ABCD为梯形，AB∥CD，∠C=60°，CD=2CB=4AB=4，点E在线段CD上，且BE⊥CD．现将△ADE沿AE翻折到△PAE的位置，使得PC=
10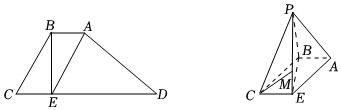
．

（1）证明：AE⊥PB；
（2）点M是线段PE上的一点（不包含端点），是否存在点M，使得二面角P-BC-M的余弦值为
6
3
？若存在，则求出
ME
PE
；若不存在，请说明理由．
组卷：244引用：7难度：0.6
解析