2023-2024学年广西南宁市武鸣区八年级(上)期中数学试卷
发布:2024/9/29 13:0:2
一、选择题:(本大题共12小题,每小题3分,共36分)
-
1.以下四大通讯运营商的企业图标中,是轴对称图形的是( )
组卷:94引用:8难度:0.9 -
2.在平面直角坐标系中,点P(-2,3)关于y轴对称的点的坐标是( )
组卷:434引用:13难度:0.9 -
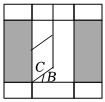 3.如图,一扇窗户打开后,用窗钩BC可将其固定,这里所运用的数学原理是( )组卷:362引用:8难度:0.7
3.如图,一扇窗户打开后,用窗钩BC可将其固定,这里所运用的数学原理是( )组卷:362引用:8难度:0.7 -
4.图中能表示△ABC的BC边上的高的是( )
组卷:3390引用:55难度:0.9 -
5.已知正多边形的一个外角等于40°,那么这个正多边形的边数为( )
组卷:1824引用:31难度:0.9 -
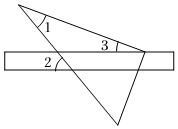 6.如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠2=50°,则∠3的度数等于( )组卷:5836引用:45难度:0.7
6.如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠2=50°,则∠3的度数等于( )组卷:5836引用:45难度:0.7 -
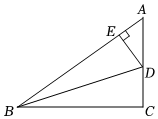 7.如图,在Rt△ABC中,∠C=90°,BD是∠ABC的平分线,DE⊥AB于点E.若AC=10,DE=4,则AD的长为( )组卷:662引用:6难度:0.7
7.如图,在Rt△ABC中,∠C=90°,BD是∠ABC的平分线,DE⊥AB于点E.若AC=10,DE=4,则AD的长为( )组卷:662引用:6难度:0.7 -
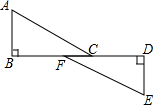 8.如图,在△ABC与△EDF中,∠B=∠D=90°,∠A=∠E,B、F、C、D在同一直线上,再添加一个下列条件,不能判断△ABC≌△EDF的是( )组卷:166引用:13难度:0.7
8.如图,在△ABC与△EDF中,∠B=∠D=90°,∠A=∠E,B、F、C、D在同一直线上,再添加一个下列条件,不能判断△ABC≌△EDF的是( )组卷:166引用:13难度:0.7
三、解答题:(本大题共8小题,共72分,解答应写出文字说明,证明过程或演算步骤)
-
 25.已知:如图,D为△ABC外角∠ACP平分线上一点,且DA=DB,DM⊥BP于点M
25.已知:如图,D为△ABC外角∠ACP平分线上一点,且DA=DB,DM⊥BP于点M
(1)若AC=6,DM=2,求△ACD的面积;
(2)求证:AC=BM+CM.组卷:2713引用:16难度:0.1 -
26.综合与探究:
(1)如图1,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.小明观察图形特征后猜想线段DE、BD和CE之间存在DE=BD+CE的数量关系,请你判断他的猜想是否正确,并说明理由.
拓展:
(2)如图2,将探究中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问探究中的结论是否成立?如成立,请你给出证明:若不成立,请说明理由.
应用:
(3)如图3,D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形;连接BD、CE,若∠BDA=∠AEC=∠BAC,请直接写出△DEF的形状是 .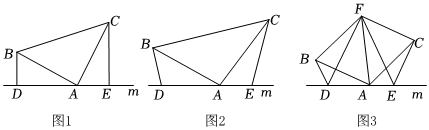 组卷:154引用:3难度:0.1
组卷:154引用:3难度:0.1


