2023-2024学年黑龙江省哈尔滨九中高三(上)开学数学试卷
发布:2024/7/12 8:0:9
一、单选题:本题共有8个小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1.设全集U=R,集合M={x|x>-1},N={x|-2<x<3},则{x|x≤-2}=( )
组卷:325引用:6难度:0.7 -
2.已知正实数m,n满足m+n=1,则
的最大值是( )m+n组卷:561引用:3难度:0.8 -
3.若p:实数a使得“∃x0∈R,
”为真命题,q:实数a使得“∀x∈[1,+∞),x2-a>0”为真命题,则p是q的( )x20+2x0+a=0组卷:104引用:5难度:0.7 -
4.函数
的图象可能是( )y=sinx•lnx2+2x2组卷:84引用:15难度:0.7 -
5.若函数f(x)=
在R上单调递增,则实数a的取值范围是( )x+ax-3,x≥4,ax-3,x<4组卷:540引用:5难度:0.7 -
6.设函数
,若f(a)+f(b)=0,则f(x)=lgx1-x的最小值为( )3b+aab组卷:76引用:8难度:0.7 -
7.已知f(x)是定义在R上的偶函数且在[0,+∞)上为减函数,若
,b=f(0.91.1),c=f(0.91.2),则( )a=f(log123)组卷:408引用:7难度:0.7
四、解答题:本题共有6个小题,共70分.
-
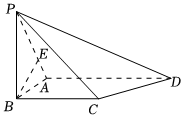 21.如图,在四棱锥P-ABCD中,平面PAB⊥平面ABCD,AB⊥BC,AD∥BC,AD=3,PA=BC=2AB=2,PB=.3
21.如图,在四棱锥P-ABCD中,平面PAB⊥平面ABCD,AB⊥BC,AD∥BC,AD=3,PA=BC=2AB=2,PB=.3
(1)求证:BC⊥PB;
(2)若点E为棱PA上不与端点重合的动点,且CE与平面PAB所成角正弦值
为,求E点到平面PCD的距离.255组卷:265引用:5难度:0.6 -
22.已知函数f(x)=xlnx.
(1)求f(x)的单调区间;
(2)若a≤-2,证明:f(x)≥ax-e-3在(0,+∞)上恒成立;
(3)若方程f(x)=b有两个实数根x1,x2,且x1<x2,求证:be+1<x2-x1<.e-3+2+3b2组卷:392引用:5难度:0.1


