2023年海南省海南中学中考数学最后仿真试卷（二）

一、选择题（本大题满分36分，每小题3分）

• 1．如果公元前500年记作-500 年，那么公元2023年应记作（　　）

  A．-2023年

  B．+1523年

  C．+2023年

  D．+2523年
  组卷：363引用：1难度：0.9

  解析

• 2．北斗卫星导航系统中有一颗中高轨道卫星，其高度大约是18500000米．数18500000用科学记数法表示为（　　）

  A．1.85×107

  B．0.185×109

  C．1.85×108

  D．18.5×107
  组卷：139引用：4难度：0.9

  解析

• 3．如图所示的几何体是由五个大小相同的小正方体搭成的，其主视图是（　　）

  A．

  B．

  C．

  D．
  组卷：14引用：2难度：0.8

  解析

• 4．当x=-1时，代数式3x+1的值是（　　）

  A．-4

  B．-2

  C．2

  D．4
  组卷：1246引用：14难度：0.9

  解析

• 5．下列计算正确的是（　　）

  A．4a-2a=2

  B．a8÷a4=a2

  C．（b2）3=b5

  D．a2•a3=a5
  组卷：112引用：3难度：0.8

  解析

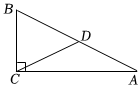• 6．如图，在Rt△ABC中，∠ACB=90°，D是AB的中点，若∠A=28°．则∠BDC的度数为（　　）

  A．26°

  B．56°

  C．52°

  D．64°
  组卷：99引用：2难度：0.6

  解析

• 7．在平面直角坐标系中，将点P（1，-2）绕原点旋转180°，得到的点Q的坐标为（　　）

  A．（-1，2）

  B．（-1，-2）

  C．（1，2）

  D．（1，-2）
  组卷：389引用：5难度：0.5

  解析

三、解答题（本大题满分72分）

• 21．如图1-1，在平行四边形ABCD中，AE=EC，AE⊥BC 于E，CG⊥AB 于G，交AE于F．
  
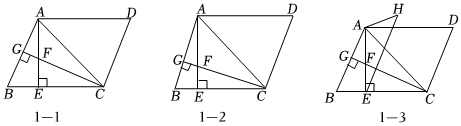
  （1）①求证：△AEB≌△CEF；②若AB=5，

  EF

  =

  5

  ，求AD的长；
  （2）如图1-2，若AF=2EF，求

  AG

  GB

  的值；
  （3）如图1-3，平行四边形ABCD外部有一H点，连接AH、EH，满足EH∥AB，∠H=∠ACE，请直接写出AG、AH和CG三者的数量关系．
  组卷：196引用：3难度：0.3

  解析

• 22．如图1-1，抛物线y=ax²+bx-3（a≠0）与x轴交于点A（-3，0）和点B（1，0），以AB为边在x轴上方作正方形ABCD，动点P从点A出发，以每秒2个单位长度的速度沿x轴的正方向匀速运动，设运动时间为t秒．连接DP，过点P作DP的垂线与y轴交于点E．
  （1）求二次函数的解析式；
  （2）当点P在线段AO上运动时，请用含t的式子表示线段OE的长度，并求出OE长度的最大值；
  （3）如图1-2，在点P开始运动的同时，动点Q从点C出发，以每秒1个单位长度的速度沿CB匀速运动，当点Q到达终点B时，点P停止运动，连接DQ．
  ①将△DCQ沿DQ翻折得到△DC′Q，当点C恰好落在抛物线的对称轴上时，求出此时的t值；
  ②如图1-3，连接DE，在P，Q运动过程中，是否存在使△DPE与△DCQ相似的t值，若存在，请直接写出t值，若不存在，请说明理由．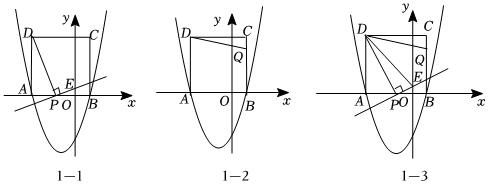
  
  组卷：117引用：1难度：0.2

  解析