2022-2023学年山东省德州市陵城区八年级（下）期中数学试卷

一、选择题（每小题4分，共48分）

• 1．下列二次根式中，最简二次根式是（　　）

  A． 1 2

  B． 4

  C． 6

  D． 8
  组卷：859引用：31难度：0.9

  解析

• 2．若代数式

  x

  -

  1

  x

  -

  2

  有意义，则x的取值范围是（　　）

  A．x＞1且x≠2

  B．x≥1

  C．x≠2

  D．x≥1且x≠2
  组卷：1300引用：86难度：0.9

  解析

• 3．海伦—秦九韶公式古希腊几何学家海伦和我国南宋数学家秦九韶都曾提出利用三角形的三边求面积的公式，称为海伦—秦九韶公式：如果一个三角形的三边长分别为a、b、c,记

  p

  =

  a

  +

  b

  +

  c

  2

  ，那么三角形的面积为：

  S

  =

  p

  （

  p

  -

  a

  ）

  （

  p

  -

  b

  ）

  （

  p

  -

  c

  ）

  ，在△ABC中，∠A，∠B，∠C所对的边分别是a、b、c,若a=5、b=8、c=7，则△ABC的面积S为（　　）

  A． 10 3

  B．30

  C． 6 6

  D．45
  组卷：164引用：3难度：0.6

  解析

• 4．下列命题，其中是真命题的为（　　）

  A．一组对边平行，另一组对边相等的四边形是平行四边形

  B．对角线互相垂直的四边形是菱形

  C．对角线相等的菱形是正方形

  D．对角线相等的四边形是矩形
  组卷：24引用：1难度：0.7

  解析

• 5．2、5、m是某三角形三边的长，则

  |

  m

  -

  3

  |

  +

  （

  m

  -

  7

  ）

  2

  等于（　　）#ZZ04

  A．2m-10

  B．10-2m

  C．10

  D．4
  组卷：762引用：8难度：0.6

  解析

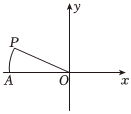• 6．如图，在平面直角坐标系中，点P的坐标为（-4，1），以点O为圆心，以OP的长为半径画弧，交x轴的负半轴于点A，则点A的横坐标介于（　　）

  A．-4和-3之间

  B．-5和-4之间

  C．3和4之间

  D．4和5之间
  组卷：86引用：1难度：0.7

  解析

• 7．如图，在菱形ABCD中，对角线AC与BD相交于点O，且AC=12，BD=16，则菱形的高AE为（　　）

  A．9.6

  B．4.8

  C．10

  D．5
  组卷：1416引用：15难度：0.6

  解析

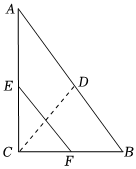• 8．如图，在Rt△ABC中，∠ACB=90°，点D，E，F分别为AB，AC，BC的中点，则DC和EF的大小关系是（　　）

  A．DC＞EF

  B．DC＜EF

  C．DC=EF

  D．无法比较
  组卷：965引用：9难度：0.7

  解析

三、解答题（7小题，共78分）

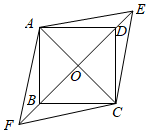• 24．如图，在▱ABCD中，对角线AC与BD相交于点O，点E，F分别在BD和DB的延长线上，且DE=BF，连接AE，CF．
  （1）求证：△ADE≌△CBF；
  （2）连接AF，CE．当BD平分∠ABC时，四边形AFCE是什么特殊四边形？请说明理由．
  组卷：688引用：19难度：0.6

  解析

• 25．如图1，四边形ABCD是正方形，点E是边BC的中点，∠AEF=90°，且EF交正方形外角平分线CF于点F．
  
  [观察猜想]（1）填空：AE与EF的数量关系

  .（提示：取AB的中点M，连接EM）
  [类比探究]（2）如图2，若把条件“点E是边BC的中点”改为“点E是边BC上的任意一点”，其余条件不变，（1）中的结论是否仍然成立？并说明理由．
  [拓展应用]（3）如图3，若把条件“点E是边BC的中点”改为“点E是边BC延长线上的一点”，其余条件仍不变，那么（1）中的结论是否成立呢？若成立写出证明过程，若不成立请说明理由．
  组卷：215引用：4难度：0.3

  解析