2022-2023学年广东省广州市荔湾区高一（下）期末数学试卷

一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

• 1．复数z满足（1+2i）z=4+3i,则复数z=（　　）

  A．-2+i

  B．-2-i

  C．2+i

  D．2-i
  组卷：96引用：6难度：0.9

  解析

• 2．已知向量

  a

  =

  （

  2

  ，

  0

  ）

  ，

  b

  =

  （

  1

  ，-

  1

  ）

  ，若

  a

  +

  λ

  b

  与

  b

  垂直，则λ等于（　　）

  A．1

  B．0

  C．-1

  D．-2
  组卷：152引用：2难度：0.7

  解析

• 3．一个小商店从一家食品有限公司购进10袋白糖，每袋白糖的标准质量是500g,为了了解这些白糖的质量情况，称出各袋白糖的质量（单位：g）如下：495，500，503，508，498，500，493，500，503，500，记10袋白糖的平均质量为

  x

  ，标准差为s,则质量位于

  x

  -

  s

  与

  x

  +

  s

  之间的白糖袋数是（　　）

  A．6

  B．7

  C．8

  D．9
  组卷：111引用：2难度：0.8

  解析

• 4．已知事件A，B，且P（A）=0.7，P（B）=0.2，则（　　）

  A．若B⊆A，则P（A∪B）=0.7，P（AB）=0.14

  B．若A，B互斥，则P（A∪B）=0.9，P（AB）=0.14

  C．若A与B相互独立，则P（A∪B）=0.9，P（AB）=0

  D．若A与B相互独立，则 P （ A B ） = 0 . 24 ， P （ A B ） = 0 . 06
  组卷：254引用：2难度：0.7

  解析

• 5．已知

  a

  ，

  b

  ，

  c

  是同一平面内的三个向量，则（　　）

  A．若 a ∥ b ， b ∥ c ，则 a ∥ c

  B．若 a 是非零向量， b ≠ c ，则 a • b = a • c 是 a ⊥ （ b - c ） 的充要条件

  C．若 a = （ 1 ，- 1 ） ， b = （ 2 ，- 3 ） ， c = （ - 3 ， 4 ） ，则 { a + b ， c } 可以作为基底

  D．若 a ， b ， c 两两的夹角相等，且 | a | = 1 ， | b | = 1 ， | c | = 3 ，则 | a + b + c | = 2
  组卷：162引用：3难度：0.7

  解析

• 6．某小区从2000户居民中随机抽取100户进行月用电量调查，发现他们的用电量都在50～350kW•h之间，进行适当的分组后（每组为左闭右开的区间），画出频率分布直方图如图所示．则（　　）
  

  A．小区用电量平均数为186.5，极差为300

  B．小区用电量中位数为171，众数为175

  C．可以估计小区居民月用电量的85%分位数约为262.5

  D．小区用电量不小于250kW•h的约有380户
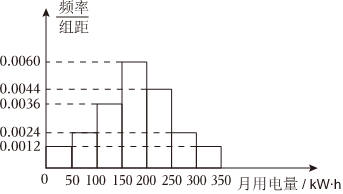  组卷：224引用：3难度：0.6

  解析

• 7．已知母线长为a的圆锥的侧面展开图为半圆，在该圆锥内放置一个圆柱，则当圆柱的侧面积最大时，圆柱的体积为（　　）

  A． 3 128 π a 3

  B． 3 64 π a 3

  C． 3 32 π a 3

  D． 3 16 π a 3
  组卷：182引用：6难度：0.5

  解析

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

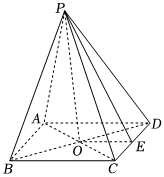• 21．如图，在四棱锥P-ABCD中，底面ABCD是边长为2的正方形，AC与BD相交于点O，E为CD的中点，PA=PB=

  2

  ，∠PAD=∠PBC，
  （1）证明：平面POE⊥平面ABCD；
  （2）当点A到平面PCD的距离最大时，求侧面PAB与底面ABCD所成二面角的大小．
  组卷：268引用：2难度：0.5

  解析

• 22．某工艺品加工厂生产线一天能生产200件某款产品，该产品市场评级规定：工艺质量指标值大于或等于10的为A等品，小于10的为B等品．厂家将A等品售价定为160元/件，B等品售价定为140元/件．
  如表是检验员在现有生产线上随机抽取的16件产品的工艺质量指标值：
  

  9.95	10.12	9.96	9.96	10.01	9.92	9.98	10.04
  10.26	9.91	10.13	10.02	9.22	10.04	10.05	9.95

  经计算得

  x

  =

  1

  16

  16

  ∑

  i

  =

  1

  x

  i

  =

  9

  .

  97

  ，

  s

  2

  =

  1

  16

  16

  ∑

  i

  =

  1

  （

  x

  i

  -

  x

  ）

  2

  =

  1

  16

  16

  ∑

  i

  =

  1

  x

  2

  i

  -

  x

  2

  =

  0

  .

  045

  ，其中x_i为抽取的第i件产品的工艺质量指标值，i=1，2，⋯，16．
  为了提高产品质量，该厂计划通过增加生产工序来改进生产工艺，已知增加生产工序每年需花费30万元，改进后该条生产线产能不变，但生产出的每件产品工艺质量指标值均提高0.05．
  （1）若将随机抽取的16件产品中各等级产品的频率视为概率，估计改进后该厂的年收益是否增加，并说明理由．（一年按365天计算）
  （2）根据随机抽取的16件产品的工艺质量指标值，估计改进后该厂一天生产的所有产品的工艺质量指标值的平均数和方差．
  组卷：89引用：2难度：0.5

  解析