2023-2024学年重庆市涪陵区部分学校高二（上）第一次月考数学试卷

一、单项选择题：本题共8小题，每小题5分，共40分．在每个小题给岀的四个选项中，只有一项是符合题目要求的．

• 1．若向量

  p

  在空间的一个单位正交基底

  a

  ，

  b

  ，

  c

  下的坐标是（1，3，2），则

  p

  在基底

  a

  +

  b

  ，

  a

  -

  b

  ，

  c

  下的坐标是（　　）

  A．（4，-2，2）

  B．（2，1，2）

  C．（2，-1，2）

  D．（1，3，2）
  组卷：186引用：6难度：0.7

  解析

• 2．已知三条射线AB，BC，BB₁不共面，四边形BB₁A₁A和四边形BB₁C₁C的对角线均互相平分，且

  A

  C

  1

  =x

  AB

  +2y

  BC

  +3z

  C

  C

  1

  ，则x+y+z的值为（　　）

  A．1

  B． 5 6

  C． 2 3

  D． 11 6
  组卷：27引用：2难度：0.8

  解析

• 3．已知直线l：（m+2）x+（m-1）y+m-1=0，若直线l与连接A（1，-2）、B（2，1）两点的线段总有公共点，则直线l的倾斜角范围为（　　）

  A． [ - π 4 ， π 4 ]	B． [ 3 π 4 ， π ）
  C． [ π 4 ， 3 π 4 ]	D． [ 0 ， π 4 ] ∪ [ 3 π 4 ， π ）
  组卷：76引用：12难度：0.8

  解析

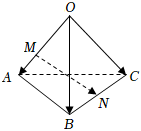• 4．如图所示，空间四边形OABC中，

  OA

  =

  a

  ，

  OB

  =

  b

  ，

  OC

  =

  c

  ，点M在OA上，且M为OA中点，N为BC中点，则

  MN

  等于（　　）

  A． - 1 2 a + 1 2 b + 1 2 c	B． 1 2 a + 1 2 b + 1 2 c
  C． 1 2 a + 1 2 b - 1 2 c	D． 1 2 a - 1 2 b + 1 2 c
  组卷：461引用：14难度：0.7

  解析

• 5．已知点（a,b）在线段3x+4y-10=0（-2≤x≤6）上，则a²+b²-2的取值范围是（　　）

  A．[2，18]

  B．[2，38]

  C．[0，38]

  D． [ 0 ， 2 10 - 2 ]
  组卷：341引用：9难度：0.7

  解析

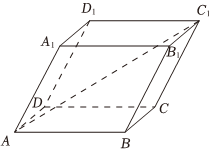• 6．如图，平行六面体ABCD-A₁B₁C₁D₁所有棱长都为1，底面ABCD为正方形，∠A₁AB=∠A₁AD=60°．则对角线AC₁的长度为（　　）

  A． 6

  B． 5

  C．2

  D． 3
  组卷：86引用：7难度：0.7

  解析

• 7．已知平面内两个定点A，B及动点P，若

  |

  PB

  |

  |

  PA

  |

  =

  λ

  （λ＞0且λ≠1），则点P的轨迹是圆．后世把这种圆称为阿波罗尼斯圆．已知O（0，0），

  Q

  （

  0

  ，

  2

  2

  ）

  ，直线l₁：kx-y+2k+3=0，直线l₂：x+ky+3k+2=0，若P为l₁，l₂的交点，则3|PO|+2|PQ|的最小值为（　　）

  A．3 3

  B． 6 - 3 2

  C． 9 - 3 2

  D． 3 + 6
  组卷：133引用：4难度：0.6

  解析

四、解答题：本题共6小题，共计70分．解答时应写出文字说明、证明过程或演算步骤．

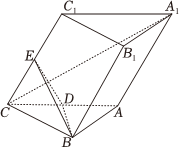• 21．如图，在三棱柱ABC-A₁B₁C₁中，底面是边长为2的等边三角形，CC₁=2，D，E分别是线段AC，CC₁的中点，C₁在平面ABC内的射影为D．
  （1）求证：A₁C⊥平面BDE；
  （2）若点F为棱B₁C₁的中点，求点F到平面BDE的距离；
  （3）若点F为线段B₁C₁上的动点（不包括端点），求锐二面角F-BD-E的余弦值的取值范围．
  
  组卷：349引用：15难度：0.5

  解析

• 22．已知圆W经过

  A

  （

  3

  ，

  3

  ）

  ，

  B

  （

  2

  ，

  2

  2

  ）

  ，

  C

  （

  2

  ，-

  2

  2

  ）

  三点．
  （1）求圆W的方程．
  （2）已知直线l与圆W交于M，N（异于A点）两点，若直线AM，AN的斜率之积为2，试问直线l是否经过定点？若经过，求出该定点坐标；若不经过，请说明理由．
  组卷：203引用：5难度：0.7

  解析