2022-2023学年浙江省杭州市西湖区弘益中学九年级（上）期中数学试卷

一、选择题（本大题共10小题，每小题3分，共30分。）

• 1．若

  b

  a

  =

  3

  2

  ，则

  b

  +

  a

  b

  等于（　　）

  A． 1 2

  B． 5 2

  C． 5 3

  D． 5 4
  组卷：8引用：1难度：0.9

  解析

• 2．若二次函数y=ax²（a≠0）的图象经过点（-2，-1），则必在该图象上的点还有（　　）

  A．（2，-1）

  B．（2，1）

  C．（-1，-2）

  D．（-2，1）
  组卷：171引用：4难度：0.6

  解析

• 3．已知⊙O的半径为5，若OP=5.5，则点P在（　　）

  A．圆内

  B．圆上

  C．圆外

  D．无法判断
  组卷：159引用：8难度：0.7

  解析

• 4．抛物线y=-2（x+1）²-2的顶点坐标是（　　）

  A．（1，2）

  B．（1，-2）

  C．（-1，2）

  D．（-1，-2）
  组卷：107引用：5难度：0.6

  解析

• 5．在⊙O中，弦AB等于圆的半径，则它所对应的圆心角的度数为（　　）

  A．120°

  B．75°

  C．60°

  D．30°
  组卷：750引用：6难度：0.7

  解析

• 6．如图，在△ABC中，点D，E分别在AB，AC上，若DE∥BC，

  AD

  AB

  =

  2

  5

  ，AE=6cm,则AC的长为（　　）

  A．9cm

  B．12cm

  C．15cm

  D．18cm
  组卷：89引用：4难度：0.6

  解析

• 7．已知抛物线y=a（x-1）²+h（a＞0）上有两点P₁（-1，y₁），P₂（t,y₂），当t≥3时，y₁与y₂大小关系为（　　）

  A．y1＜y2

  B．y1≤y2

  C．y1＞y2

  D．y1≥y2
  组卷：261引用：4难度：0.6

  解析

三、解答题（本大题共7小题，共66分.解答应写出必要的文字说明、证明过程或演算步骤）

• 22．在平面直角坐标系中，设二次函数y₁=mx²-6mx+8m（m为常数）．
  （1）若函数y₁经过点（1，3），求函数y₁的表达式；
  （2）若m＜0，当x

  ＜

  a

  2

  时，此二次函数y随x的增大而增大，求a的取值范围；
  （3）已知一次函数y₂=x-2，当y₁•y₂＞0时，求x的取值范围．
  组卷：1423引用：3难度：0.3

  解析

• 23．如图1，在矩形ABCD中，AC与BD交于点O，E为AD上一点，CE与BD交于点F．
  
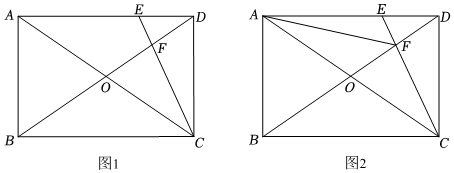
  （1）若AE=CE，BD⊥CE，①求∠DEC的度数．②如图2，连接AF，当BC=3时，求AF的值．
  （2）设

  DE

  AD

  =

  k

  （

  0

  ＜

  k

  ＜

  1

  ）

  ，记△CBF的面积为S₁，四边形ABFE的面积为S₂，求

  S

  2

  S

  1

  的最大值．
  组卷：222引用：2难度：0.4

  解析