2021年湖南省株洲市芦淞区中考数学模拟试卷
发布:2024/6/13 8:0:9
一、选择题(本题共10小题,每小题4分,满分40分)
-
1.16的平方根是( )
组卷:108引用:16难度:0.9 -
2.将下列四个数表示在数轴上,它们对应的点中,离原点最近的是( )
组卷:18引用:1难度:0.9 -
3.围棋起源于中国,古代称之为“弈”,至今已有四千多年的历史.下列由黑白棋子摆成的图案是中心对称图形的是( )
组卷:760引用:36难度:0.9 -
4.下列运算正确的是( )
组卷:983引用:19难度:0.8 -
5.一组数据:2,3,4,x中,若中位数与平均数相等,则数x不可能是( )
组卷:504引用:13难度:0.9 -
6.关于x的方程
的解为2,则m的值是( )32x-m=1组卷:9引用:1难度:0.7 -
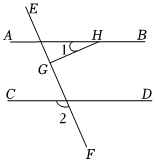 7.如图,AB∥CD,CH⊥EF于G,∠1=28°,则∠2的度数为( )组卷:16引用:1难度:0.6
7.如图,AB∥CD,CH⊥EF于G,∠1=28°,则∠2的度数为( )组卷:16引用:1难度:0.6 -
 8.如图,△ABC与△DEF位似,点O为位似中心.已知OA:OD=1:2,则△ABC与△DEF的面积比为( )组卷:2787引用:44难度:0.7
8.如图,△ABC与△DEF位似,点O为位似中心.已知OA:OD=1:2,则△ABC与△DEF的面积比为( )组卷:2787引用:44难度:0.7
三、解答题(本题共8个小题,满分78,需要写出必要的推理与解题过程)
-
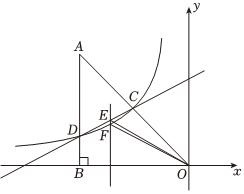 25.如图,在平面直角坐标系xOy中,△ABO的边AB垂直于x轴,垂足为点B,反比例函数的图象经过AO的中点C,交AB于点D.若点D的坐标为(-4,n),且AD=3.
25.如图,在平面直角坐标系xOy中,△ABO的边AB垂直于x轴,垂足为点B,反比例函数的图象经过AO的中点C,交AB于点D.若点D的坐标为(-4,n),且AD=3.
(1)求反比例函数的解析式;y=kx
(2)求经过C,D两点的直线所对应的函数解析式;
(3)设点E是线段CD上的动点(不与点C,D重合),过点E且平行于y轴的直线l与反比例函数的图象交于点F,求△OEF面积的最大值.组卷:106引用:2难度:0.2 -
26.对于抛物线y=ax2+bx+c(a≠0),如果抛物线与x轴有两个交点,我们就将它的顶点以及它与x轴的两个交点构成的三角形称为该抛物线的“内接三角形”.
(1)若抛物线有“内接三角形”,求m的取值范围.y=x2+3x-m
(2)如图1,抛物线y=ax2-6x+c与x轴的交点分别为点A、点B(点A在点B左边),顶点为点D,该抛物线的“内接三角形”△ABD为等边三角形.
①求ac的值;
②如图2,若该抛物线经过点(0,6),∠BAD的平分线交BD于点P,点M为射线AB上一点.连接直线PM交射线AD于点N,求的值.1AM+1AN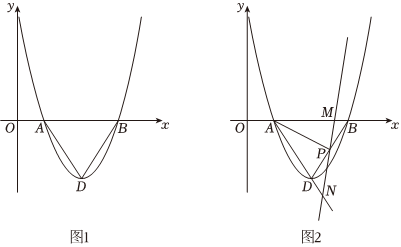 组卷:99引用:2难度:0.3
组卷:99引用:2难度:0.3


