2023-2024学年四川省眉山市彭山一中高二(上)开学数学试卷
发布:2024/8/11 6:0:3
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1.若复数
(i为虚数单位),则z的虚部为( )z=1+i1-i-2i组卷:28引用:2难度:0.8 -
2.甲、乙两名运动员进入男子羽毛球单打决赛,假设比赛打满3局,赢得2局或3局者胜出,用计算机产生1~5之间的随机数,当出现随机数1,2,3时,表示一局比赛甲获胜;否则,乙获胜.由于要比赛3局,所以每3个随机数为一组,产生20组随机数:
423 123 423 344 114 453 525 332 152 342
534 443 512 541 125 432 334 151 314 354
据此估计甲获得冠军的概率为( )组卷:166引用:6难度:0.9 -
3.已知第二象限角α的终边与单位圆交于
,则sin2α=( )P(m,35)组卷:106引用:5难度:0.7 -
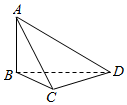 4.在我国古代数学名著《九章算术》中,将四个面都为直角三角形的四面体称为鳖臑,如图,在鳖臑ABCD中,AB⊥平面BCD,且AB=BC=CD,则异面直线AC与BD所成角的余弦值为( )组卷:560引用:20难度:0.7
4.在我国古代数学名著《九章算术》中,将四个面都为直角三角形的四面体称为鳖臑,如图,在鳖臑ABCD中,AB⊥平面BCD,且AB=BC=CD,则异面直线AC与BD所成角的余弦值为( )组卷:560引用:20难度:0.7 -
5.已知△ABC是边长为a的等边三角形,点D,E,F分别是边AB,BC,AC的中点,连接DE并延长到点M,使得DE=2EM,连接DF并延长到点N,使得DF=FN,则
的值为( )AM•BN组卷:48引用:3难度:0.7 -
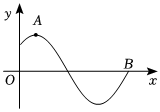 6.已知函数的部分图象如下所示,其中f(x)=2cos(ωx+φ)(ω>0,|φ|<π2),为了得到g(x)=2sin2x的图象,需将( )A(π12,2),B(7π12,0)组卷:266引用:5难度:0.8
6.已知函数的部分图象如下所示,其中f(x)=2cos(ωx+φ)(ω>0,|φ|<π2),为了得到g(x)=2sin2x的图象,需将( )A(π12,2),B(7π12,0)组卷:266引用:5难度:0.8 -
7.已知函数
(ω>0),若f(x)在区间[0,π)内有且仅有3个零点和3条对称轴,则ω的取值范围是( )f(x)=2cos(ωx+π6)组卷:492引用:11难度:0.6
四、解答题(本大题共6小题,共70分,17题10分,18—22题各12分,解答应写出文字说明、证明过程或演算步骤)
-
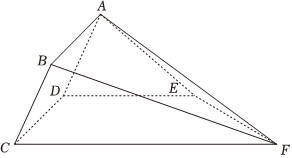 21.如图,多面体ABCDEF中,四边形ABCD为平行四边形,AD=2,DC=2,四边形DCFE为梯形,DE∥CF,CD⊥DE,DE=3,CF=6,∠ADE=45°,平面ADE⊥平面DCFE.2
21.如图,多面体ABCDEF中,四边形ABCD为平行四边形,AD=2,DC=2,四边形DCFE为梯形,DE∥CF,CD⊥DE,DE=3,CF=6,∠ADE=45°,平面ADE⊥平面DCFE.2
(1)求证:AE∥平面BCF;
(2)求直线AC与平面CDEF所成角的正弦值;
(3)求点F到平面ABCD的距离.组卷:209引用:5难度:0.4 -
22.如图1,在ABC中,∠C=90°,AB=4,BC=2,D是AC中点,作DE⊥AB于E,将△ADE沿直线DE折起到△PDE所处的位置,连接PB,PC,如图2.
(1)若,求证:PE⊥BC;PB=342
(2)若二面角P-DE-A为锐角,且二面角P-BC-E的正切值为,求PB的长.269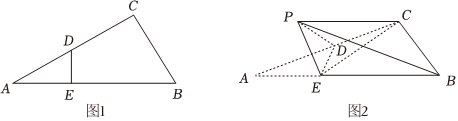 组卷:150引用:5难度:0.5
组卷:150引用:5难度:0.5


