2021-2022学年重庆市西南大学附中高一（上）期中数学试卷

一、单项选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

• 1．已知集合A={x||x-1|＜2}，B={x|x²-2x-3＜0}，则A∩B=（　　）

  A．{x|-1＜x＜3}

  B．{x|-2＜x＜3}

  C．{x|-2＜x＜-1}

  D．∅
  组卷：55引用：2难度：0.8

  解析

• 2．下列图形是函数图像的是（　　）

  A．	B．
  C．	D．
  组卷：335引用：4难度：0.9

  解析

• 3．已知a＞b＞0，d＜c,其中a,b,c,d均为实数，则一定有（　　）

  A．ac＞bd＞0

  B．ac＞bd

  C．a+c＞b+d＞0

  D．a+c＞b+d
  组卷：59引用：5难度：0.8

  解析

• 4．函数

  f

  （

  x

  ）

  =

  1

  -

  1

  x

  -

  2

  的值域为（　　）

  A．{y|y≠1}

  B．y≠1

  C．y≠2

  D．{y|y≠2}
  组卷：12引用：1难度：0.8

  解析

• 5．已知函数f（x）=

  1 x ， （ x ≤ - 1 ）

  a x 2 + 4 ax + 1 + 4 a , （ x ＞ - 1 ）

  是R上的递减函数，则实数a的取值范围是（　　）

  A． a ≤ - 2 3

  B． a ≤ - 3 8

  C．a≤-2

  D．a≤-1
  组卷：299引用：5难度：0.7

  解析

• 6．已知函数f（x）=ax³-bx+2，若f（2）=5，则f（-2）=（　　）

  A．-1

  B．1

  C．3

  D．-3
  组卷：25引用：3难度：0.7

  解析

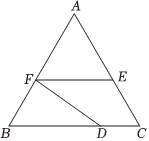• 7．某工厂要在一个正三角形ABC的钢板上切割一个四边形的材料DCEF来加工，若AB=2，DC=

  2

  3

  ，DC∥EF（如图），则四边形DCEF面积最大值为（　　）

  A． 5 3 12

  B． 4 3 9

  C． 3

  D． 5 2
  组卷：7引用：1难度：0.6

  解析

四、解答题：本大题共6小题，共70分．解答应写出必要的文字说明、证明过程或演算步骤．

• 21．已知函数y=f（x）的定义域为R，且对一切x∈R都有f（x）+2f（-x）=3ax²-（a²+1）x+3a恒成立．
  （1）求函数y=f（x）的解析式；
  （2）求关于x的不等式f（x）＞0的解集．
  组卷：4引用：2难度：0.7

  解析

• 22．已知函数

  f

  （

  x

  ）

  =

  2

  x

  -

  1

  2

  x

  +

  1

  ．
  （1）判断f（x）的单调性，并用定义法证明；
  （2）设函数g（x）=f（|x|），且存在x∈[-1，1]，使得3g（-4^x+（a-1）2^x+a）＜5成立，求实数a的取值范围．
  组卷：20引用：1难度：0.4

  解析