当前位置：试卷中心 > 试卷详情

2023-2024学年河南省周口恒大中学高三（上）月考数学试卷（10月份）

发布：2024/9/23 14:0:9

一、单项选择题（每小题5分，共40分）

1．抛物线y²=8x上两点M、N到焦点F的距离分别是d₁，d₂，若d₁+d₂=5，则线段MN的中点P到y轴的距离为（　　）
A．
5
2
B．5 C．
1
2
D．1
组卷：106引用：1难度：0.7
解析
2．已知直线：A₁x+B₁y+C₁=0（C₁≠0）与直线l₂：A₂x+B₂y+C₂=0（C₂≠0）交于点M，O为坐标原点，则直线OM的方程为（　　）
A．
（
A
1
C
1
-
A
2
C
2
）
x
+
（
B
1
C
1
-
B
2
C
2
）
y
=
0
B．
（
A
1
C
1
-
A
2
C
2
）
x
-
（
B
1
C
1
-
B
2
C
2
）
y
=
0
C．
（
C
1
A
1
-
C
2
A
2
）
x
+
（
C
1
B
1
-
C
2
B
2
）
y
=
0
D．
（
C
1
A
1
-
C
2
A
2
）
x
-
（
C
1
B
1
-
C
2
B
2
）
y
=
0
组卷：291引用：4难度：0.5
解析
3．已知f（x）=sinxcosx,则f（x）的最小值与最小正周期分别是（　　）
A．
-
1
2
，π B．-1，π C．
-
1
2
，2π D．-2，2π
组卷：139引用：6难度：0.7
解析
4．如果一个水平放置的图形的斜二测直观图是一个底角为45°，上底为1，腰为
2
的等腰梯形，那么原平面图形的面积是（　　）
A．
2
2
B．
2
2
C．
4
2
D．
8
2
组卷：295引用：6难度：0.7
解析
5．已知向量
a
≠
e
，|
e
|=1，对任意t∈R，恒有|
a
-t
e
|≥|
a
-
e
|，则（　　）
A．
a
⊥
e
B．
a
⊥（
a
-
e
）
C．
e
⊥（
a
-
e
） D．（
a
+
e
）⊥（
a
-
e
）
组卷：1248引用：21难度：0.9
解析
6．已知sin（
π
6
-α）=
1
2
，那么cos（
2
π
3
-α）=（　　）
A．
3
2
B．-
3
2
C．
1
2
D．-
1
2
组卷：36引用：2难度：0.9
解析
7．给定四个函数：①y=x³；②y=3x+1；③y=2x,x∈[-1，2]；④
y
=
1
x
，其中是奇函数的有（　　）
A．1个 B．2个 C．3个 D．4个
组卷：133引用：1难度：0.8
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题（共6小题，共计70分.第17题10分，第18---22题，每题12分）

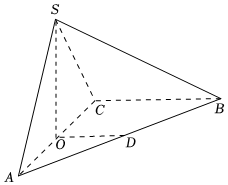21．在三棱锥S-ABC中，平面SAC⊥平面ABC，且△SAC是正三角形，O是AC的中点，D是AB的中点．
（Ⅰ）求证：OD∥平面SBC；
（Ⅱ）求证：SO⊥AB．
组卷：146引用：4难度：0.3
解析
22．已知：函数
f
（
x
）
=
a
-
2
x
．
（1）若函数f（x）为奇函数，求a的值；
（2）试用定义判断函数f（x）在区间（0，+∞）上的单调性．
组卷：153引用：2难度：0.7
解析