2022-2023学年浙江省杭州市西湖区紫金港中学九年级（上）期中数学试卷

一、选择题（每题3分，共30分）

• 1．如果3a=2b,那么

  a

  b

  等于（　　）

  A． 2 3

  B． 2 5

  C． 3 2

  D． 5 3
  组卷：20引用：1难度：0.8

  解析

• 2．对于y=2（x-3）²+2的图象，下列叙述正确的是（　　）

  A．顶点坐标为（-3，2）

  B．对称轴为y=3

  C．当x≥3时y随x增大而增大

  D．当x≤3时y随x增大而增大
  组卷：84引用：3难度：0.9

  解析

• 3．在一个不透明的盒子中装有8个白球，若干个黄球，它们除颜色不同外，其余均相同，若从中随机摸出一个球为白球的概率是

  2

  3

  ，则黄球的个数为（　　）

  A．16

  B．12

  C．8

  D．4
  组卷：510引用：23难度：0.9

  解析

• 4．在直角三角形ABC中，∠C=90°，AC=3，AB=5．若以点C为圆心，画一个半径为3的圆，则点A，点B和⊙C的相互位置关系为（　　）

  A．点A，点B均在⊙C内	B．点A，点B均在⊙C外
  C．点A，点B均在⊙C上	D．点A在⊙C上，点B在⊙C外
  组卷：1066引用：4难度：0.9

  解析

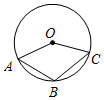• 5．如图，点A、B、C都在⊙O上，若∠AOC=140°，则∠B的度数是（　　）

  A．70°

  B．80°

  C．110°

  D．140°
  组卷：1486引用：13难度：0.7

  解析

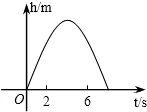• 6．竖直向上发射的小球的高度h（m）关于运动时间t（s）的函数表达式为h=at²+bt,其图象如图所示，若小球在发射后第2秒与第6秒时的高度相等，则下列时刻中小球的高度最高的是（　　）

  A．第3秒

  B．第3.5秒

  C．第4.2秒

  D．第6.5秒
  组卷：1293引用：19难度：0.9

  解析

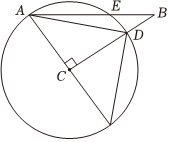• 7．Rt△ABC中，∠C=90°，AC=6，BC=8，以点C为圆心，CA为半径的圆与AB、BC分别交于点E、D，则AE的长为（　　）

  A． 72 5

  B． 12 5

  C． 18 5

  D． 36 5
  组卷：127引用：1难度：0.9

  解析

三、解答题：（共66分）

• 22．设一次函数y₁=x+a+b和二次函数y₂=x（x+a）+b.
  （1）若y₁，y₂的图象都经过点（-2，1），求这两个函数的表达式．
  （2）求证：y₁，y₂的图象必有交点．
  （3）若a＞0，y₁，y₂的图象交于点（x₁，m），（x₂，n）（x₁＜x₂），设（x₃，n）为y₂图象上一点（x₁≠x₂），求x₃-x₁的值．
  组卷：221引用：1难度：0.5

  解析

• 23．已知⊙O为△ACD的外接圆，AD=CD．
  （1）如图1，延长AD至点B，使BD=AD，连接CB．
  ①求证：△ABC为直角三角形；
  ②若⊙O的半径为4，AD=5，求BC的值；
  （2）如图2，若∠ADC=90°，E为⊙O上的一点，且点D，E位于AC两侧，作△ADE关于AD对称的图形△ADQ，连接QC，试猜想QA，QC，QD三者之间的数量关系并给予证明．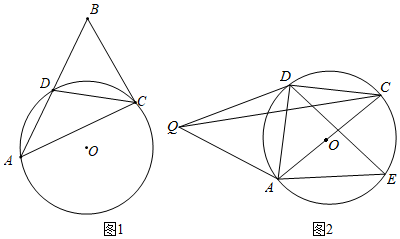
  
  组卷：3149引用：10难度：0.2

  解析