2023-2024学年江苏省盐城中学高二（上）学情检测数学试卷（8月份）

一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．一条直线过点A（-1，0）和B（2，3），则该直线的倾斜角为（　　）

  A．30°

  B．45°

  C．60°

  D．90°
  组卷：210引用：11难度：0.7

  解析

• 2．已知复数z=（1+i）²（i为虚数单位），则复数z的虚部为（　　）

  A．2

  B．-2

  C．2i

  D．-2i
  组卷：41引用：4难度：0.8

  解析

• 3．已知过点A（-2，m）和点B（m,4）的直线为l₁，

  l

  2

  ：

  y

  =

  -

  2

  x

  +

  1

  ，

  l

  3

  ：

  y

  =

  -

  1

  n

  x

  -

  1

  n

  ．若l₁∥l₂，l₂⊥l₃，则m+n的值为（　　）

  A．-10

  B．-2

  C．0

  D．8
  组卷：263引用：6难度：0.9

  解析

• 4．直线l按向量

  a

  =

  （

  -

  3

  ，

  1

  ）

  平移后得直线l'，设直线l与l'之间的距离为d,则d的范围是（　　）

  A． [ 10 ， + ∞ ）

  B． [ 0 ， 10 ]

  C．[1，3]

  D．[0，10]
  组卷：72引用：3难度：0.8

  解析

• 5．苏格兰数学家纳皮尔发明了对数，在此基础上，布里格斯制作了第一个常用对数表，对数是简化大数运算的有效工具．若一个20位整数m的32次方根仍是一个整数n,则根据下表数据，可知n=（　　）
  

  x	2	3	7
  lgx	0.30	0.48	0.85

  A．3

  B．4

  C．6

  D．7
  组卷：75引用：3难度：0.8

  解析

• 6．若直线y=x+b与曲线

  y

  =

  3

  -

  4

  x

  -

  x

  2

  有公共点，则b的取值范围是（　　）

  A．[ - 1 ， 1 + 2 2 ]

  B．[ 1 - 2 2 ， 1 + 2 2 ]

  C．[ 1 - 2 2 ， 3 ]

  D．[ 1 - 2 ， 3 ]
  组卷：383引用：1难度：0.6

  解析

• 7．在三棱锥P-ABC中，△ABC是等腰直角三角形，AB=BC=2，PC=AC，且PC⊥平面ABC，则三棱锥的外接球的表面积为（　　）

  A．16π

  B．8π

  C． 4 3 π

  D． 32 3 π
  组卷：246引用：3难度：0.7

  解析

四、解答题：本题共6小题，17题10分，其余每小题10分共70分.解答应写出文字说明、证明过程或演算步骤

• 21．已知函数

  f

  （

  x

  ）

  =

  si

  n

  2

  ωx

  +

  2

  3

  sinωxcosωx

  -

  co

  s

  2

  ωx

  （

  ω

  ＞

  0

  ）

  
  （1）若y=f（x）的最小正周期为π，求y=f（x），

  x

  ∈

  （

  0

  ，

  π

  2

  ）

  的单调区间；
  （2）将（1）中的函数f（x）图像上所有的点向右平移

  φ

  （

  φ

  ∈

  [

  0

  ，

  π

  2

  ]

  ）

  个单位长度，得到函数y=g（x），且y=g（x）图像关于x=0对称．若对于任意的实数a,函数y=g（λx），

  x

  ∈

  [

  a

  ,

  a

  +

  π

  3

  ]

  与y=1的公共点个数不少于6个且不多于10个，求正实数λ的取值范围．
  组卷：22引用：2难度：0.5

  解析

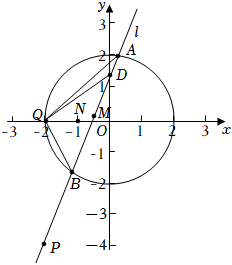• 22．如图，在平面直角坐标系xOy中，已知点P（-2，-4），圆O：x²+y²=4与x轴的负半轴的交点是Q，过点P的直线l与圆O交于不同的两点A，B．
  （1）设直线QA，QB的斜率分别是k₁，k₂，求k₁+k₂的值：
  （2）设AB的中点为M，点N（-1，0），若MN=

  1

  4

  OM，求△QAB的面积．
  组卷：80引用：3难度：0.4

  解析