2022-2023学年湖南省长沙市开福区立信中学九年级（上）期中数学试卷

一、选择题（本大题10道小题，每题3分，共30分）

• 1．下列各数中，是无理数的是（　　）

  A．3.1415

  B． 4

  C． 22 7

  D． 6
  组卷：1093引用：44难度：0.8

  解析

• 2．围棋起源于中国．古代称之为“弈”，至今已有4000多年历史．2017年5月，世界围棋冠军柯洁与人工智能机器人AlphaGo进行了围棋人机大战．截取对战机棋谱中的四个部分，由黑白棋子摆成的图案是中心对称的是（　　）

  A．

  B．

  C．

  D．
  组卷：247引用：13难度：0.8

  解析

• 3．下列各运算中，正确的运算是（　　）

  A． 2 + 3 = 5	B．（2a）3=8a3
  C．a8÷a4=a2	D．（a-b）2=a2-b2
  组卷：655引用：7难度：0.7

  解析

• 4．如图，直线a∥b,将三角尺的直角顶点放在直线b上，若∠1=35°，则∠2等于（　　）

  A．45°

  B．55°

  C．35°

  D．65°
  组卷：1567引用：15难度：0.7

  解析

• 5．若将点A（1，3）向左平移2个单位得到点B，则点B的坐标为（　　）

  A．（-1，3）

  B．（1，1）

  C．（3，3）

  D．（1，5）
  组卷：27引用：2难度：0.7

  解析

• 6．下列关于圆的说法，正确的是（　　）

  A．在同圆或等圆中，相等的弦所对的圆周角相等

  B．平分弦的直径垂直于弦

  C．圆的每一条直径所在的直线都是它的对称轴

  D．过三点可以作一个圆
  组卷：785引用：8难度：0.6

  解析

• 7．下列函数中不是反比例函数的是（　　）

  A．y= 3 x

  B．y=3x-1

  C．xy=1

  D． y = - x 3
  组卷：618引用：4难度：0.7

  解析

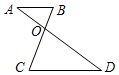• 8．如图，AD、BC相交于点O，由下列条件不能判定△AOB与△DOC相似的是（　　）

  A．AB∥CD

  B．∠A=∠D

  C． OA OD = OB OC

  D． OA OD = AB CD
  组卷：3599引用：31难度：0.6

  解析

三、解答题（本大题共9个小题，分值6+6+6+8+8+9+9+10+10=72分）

• 24．定义：在平面直角坐标系中，若对于任意两点A（x₁，y₁）、B（x₂，y₂），都有x₁+x₂=y₁+y₂，则称A、B两点互为“互信点”．
  （1）若点A（2，3），那么B（-1，2）、C（1，0）、D（-3，-2）中，点A的“互信点”是

  ；
  （2）若点A在直线y=x+1上，点P在双曲线

  y

  =

  2

  x

  上，且A、P两点互为“互信点”．请求出点P的坐标；
  （3）已知抛物线y=ax²+2bx+3c（a≠0，a,b,c为常数）．顶点为M点，与x轴交于E、F两点，与直线y=bx+2c交于P、Q两点．若满足：①抛物线过点（0，-3）；②△MEF为等边三角形；③P、Q两点互为“互信点”．求b-a+c的值．
  组卷：265引用：2难度：0.5

  解析

• 25．抛物线

  y

  =

  -

  1

  2

  x

  2

  +

  bx

  +

  c

  与x轴交于A（-1，0），B两点，与y轴交于点C（0，2）．
  （1）求抛物线的解析式；
  （2）①直接写出△AOC外接圆的圆心坐标；
  ②如图1，点E在第一象限抛物线上，连接BE，CD∥BE交OB于点D，连接DE，△DBE面积为4，求E点坐标．
  （3）如图2，将直线AC绕点P（m,n）顺时针旋转90°后，得到的对应直线FG与抛物线有唯一公共点，求m与n的数量关系．
  组卷：223引用：2难度：0.5

  解析