2023年湖北省武汉市华中师大一附中高考数学适应性试卷（5月份）

一、单项选择题：本题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．若2-z=zi,则|

  z

  +i|=（　　）

  A．1

  B．2

  C． 2

  D． 5
  组卷：49引用：1难度：0.8

  解析

• 2．若集合A={x|log₂x＜1}，B={x||x|≥1}，则A∪∁_RB=（　　）

  A．{x|0＜x＜1}	B．{x|-1＜x＜2}
  C．{x|-1＜x＜0或0＜x＜2}	D．{x|x＜2}
  组卷：111引用：2难度：0.8

  解析

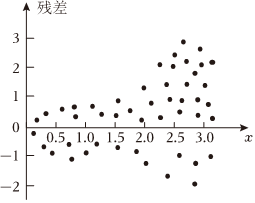• 3．根据变量Y和x的成对样本数据，用一元线性回归模型

  Y = bx + a + e

  E （ e ） = 0 ， D （ e ） = σ 2

  得到经验回归模型

  ̂

  y

  =

  ̂

  b

  x

  +

  ̂

  a

  ，对应的残差如图所示，模型误差（　　）

  A．满足一元线性回归模型的所有假设

  B．不满足一元线性回归模型的E（e）=0的假设

  C．不满足一元线性回归模型的D（e）=σ2假设

  D．不满足一元线性回归模型的E（e）=0和D（e）=σ2的假设
  组卷：323引用：7难度：0.6

  解析

• 4．设{a_n}是等比数列，m,n,s,t∈N^*，则“m+n=s+t”是“a_m•a_n=a_s•a_t”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分也不必要条件
  组卷：66引用：7难度：0.9

  解析

• 5．（

  sinθ

  x

  -x+1）⁶的展开式中x⁴的系数为12，则cos2θ=（　　）

  A． 1 4

  B． - 1 2

  C． 1 2

  D． 3 4
  组卷：144引用：3难度：0.7

  解析

• 6．当0＜x＜1时，下列不等式正确的是（　　）

  A．（ sinx x ）2＜ sin x 2 x 2 ＜ sinx x

  B． sin x 2 x 2 ＜（ sinx x ）2＜ sinx x

  C．（ sinx x ）2＜ sinx x ＜ sin x 2 x 2

  D． sinx x ＜（ sinx x ）2＜ sin x 2 x 2
  组卷：222引用：4难度：0.9

  解析

• 7．正方形ABB₁A₁的边长为12，其内有两点P、Q，点P到边AA₁，A₁B₁的距离分别为3，2，点Q到边BB₁，AB的距离也是3和2．现将正方形卷成一个圆柱，使得AB和A₁B₁重合（如图）．则此时P、Q两点间的距离为（　　）

  A． 6 1 + π 2 π

  B． 6 2 + π 2 π

  C． 6 3 + π 2 π

  D． 6 4 + π 2 π
  组卷：121引用：6难度：0.5

  解析

四、解答题：本题共6小题，共70分，解答应写出必要的文字说明、证明过程或演算步骤.

• 21．已知抛物线T的顶点在原点，对称轴为坐标轴，且过（-2，1），（1，

  1

  4

  ），（-2，-2），（3，-2）四点中的两点．
  （1）求抛物线T的方程；
  （2）已知圆x²+（y-2）²=3，过点P（m,1）（m≠±

  3

  ）作圆的两条切线，分别交抛物线T于A（x₁，y₁），B（x₂，y₂）和C（x₃，y₃），D（x₄，y₄）四个点，试判断x₁x₂x₃x₄是否是定值？若是定值，求出定值，若不是定值，请说明理由．
  组卷：125引用：1难度：0.5

  解析

• 22．已知函数f（x）=ae^2x-1-x²（lnx+

  1

  2

  ）．
  （1）若a=0，证明：f（x）≥

  x

  2

  2

  -x³；
  （2）设g（x）=xf（x）+

  x

  2

  e

  x

  ，若∀x＞1，xg（

  lnx

  x

  -

  1

  ）＜g（

  xlnx

  x

  -

  1

  ）恒成立，求实数a的取值范围．
  组卷：150引用：8难度：0.5

  解析