当前位置：试卷中心 > 试卷详情

2022-2023学年河南省南阳市宛城区金华中学八年级（上）第一次月考数学试卷

发布：2024/8/19 8:0:2

一、选择题（共30分）

1．小明在作业本上做了4道题①
3
-
125
=-5；②±
16
=4；③
3
81
=9；④
（
-
6
）
2
=-6，他做对的题有（　　）
A．1道 B．2道 C．3道 D．4道
组卷：811引用：16难度：0.8
解析
2．下列说法错误的是（　　）
A．3的平方根是
3
B．-1的立方根是-1
C．0.1是0.01的一个平方根
D．算术平方根是本身的数只有0和1
组卷：1887引用：17难度：0.9
解析
3．下列各式中，计算正确的是（　　）
A．a³+a²=a⁵ B．a³-a²=a C．（a²）³=a⁵ D．a²•a³=a⁵
组卷：777引用：28难度：0.7
解析
4．已知3^2m=5，3²ⁿ=10，则9^m-n+1的值是（　　）
A．
9
2
B．
3
2
C．-2 D．4
组卷：1992引用：16难度：0.6
解析
5．电子文件的大小常用B，KB，MB，GB等作为单位，其中1GB=2¹⁰MB，1MB=2¹⁰KB，1KB=2¹⁰B．某视频文件的大小约为1GB，1GB等于（　　）
A．2³⁰B B．8³⁰B C．8×10¹⁰B D．2×10³⁰B
组卷：3600引用：41难度：0.8
解析
6．若单项式-3x^4a-by²与
1
3
x
3
y
a
+
b
是同类项，那么这两个单项式的积是（　　）
A．x⁶y⁴ B．-x³y² C．-
8
3
x
3
y
2
D．-x⁶y⁴
组卷：417引用：4难度：0.5
解析
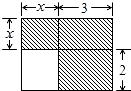7．下面四个整式中，不能表示图中阴影部分面积的是（　　）
A．x²+5x B．x（x+3）+6
C．3（x+2）+x² D．（x+3）（x+2）-2x
组卷：9427引用：116难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（共75分）

22．（1）比较下列两个算式的结果的大小（在横线上选填“＞”“=”或“＜”）
①3²+4²
2×3×4；
②（
1
3
）²+（
1
4
）²
2×
1
3
×
1
4
；
③（-2）²+（-3）²
2×（-2）×（-3）；
④（-4）²+（-4）²
2×（-4）×（-4）…
（2）观察并纳（1）中的规律，用含a,b的一个关系式把你的发现表示出来．
组卷：17引用：3难度：0.7
解析
23．材料1：著名的瑞士数学家欧拉曾指出：可以表示为四个整数平方之和的甲、乙两数相乘，其乘积仍然可以表示为四个整数平方之和，即（a²+b²+c²+d²）（e²+f²+g²+h²）=A²+B²+C²+D²，这就是著名的欧拉恒等式，有人称这样的数为“不变心的数”．
实际上，上述结论可减弱为：可以表示为两个整数平方之和的甲、乙两数相乘，其乘积仍然可以表示为两个整数平方之和，即（a²+b²）（c²+d²）=A²+B²
材料2：在数学思想中，有种解题技巧称之为“无中生有”．
例如问题：将代数式x²-y²+
1
x
2
-
1
y
2
改成两个平方之和的形式．
解：原式=（x²+
1
x
2
+2•x•
1
x
）-（y²+
1
y
2
+2•y•
1
y
）=（x+
1
x
）²-（y+
1
y
）²．
解决问题：
（1）试将（1²+2²）（1²+3²）改写成两个不相等的整数平方之和的形式．（1²+2²）（1²+3²）=
；
（2）请你灵活运用“无中生有”的解题技巧解决“不变心的数”问题：将代数式（a²+b²）（c²+d²）改成两个整数平方之和的形式（其中a、b、c、d均为整数），并给出详细的推导过程．
组卷：34引用：2难度：0.6
解析