2022-2023学年河北省邢台市威县三中八年级（上）期中数学试卷
发布：2024/8/27 12:0:9
一、选择题。（本大题共16个小题，1～10小题每题3分，11～16小题每题2分，共42分.在每小题给出的四个选项中，只有一项是符合题目要求的）
-
1．围棋起源于中国，古代称之为“弈”，至今已有四千多年的历史，下列由黑白棋子摆成的图案是轴对称图形的是（ ）
组卷：3620引用：89难度：0.9 -
2．嘉嘉和淇淇到学校的直线距离分别是5km和3km,那么嘉嘉和淇淇的直线距离不可能是（ ）
组卷：290引用：8难度：0.8 -
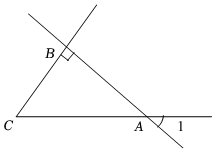3．如图，∠1=40°，则∠C的度数为（ ）组卷：400引用：5难度：0.8 -
4．如图，BE，CD是△ABC的高，且BD=EC，直接判定△BCD≌△CBE的依据是（ ）组卷：260引用：7难度：0.7 -
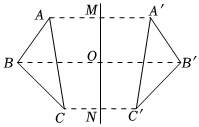5．如图，若△ABC与△A′B′C′关于直线MN对称，BB′交MN于点O，则下列说法中不一定正确的是（ ）组卷：557引用：37难度：0.9 -
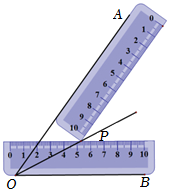6．两把相同的长方形直尺按如图所示方式摆放，记两把直尺的接触点为P，其中一把直尺边缘和射线OA重合，另一把直尺的下边缘与射线OB重合，连接OP并延长．若∠BOP=28°，则∠AOB的度数为（ ）组卷：197引用：9难度：0.7 -
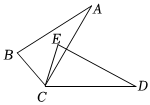7．如图，已知△ABC≌△DEC，点B和点E是对应顶点．若∠BCD=130°，∠ACE=10°，则∠ACD的度数为（ ）组卷：51引用：2难度：0.6 -
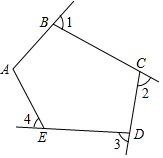8．如图，五边形ABCDE的一个内角∠A=110°，则∠1+∠2+∠3+∠4等于（ ）组卷：1971引用：22难度：0.9
三、解答题。（本大题共7个小题，共69分.解答应写出文字说明、证明过程或演算步骤）
-
25．在△ABC中，∠ACB＞∠ABC，D，E分别是边BC和BC延长线上的点，连接AD，AE，∠CAE=∠B．
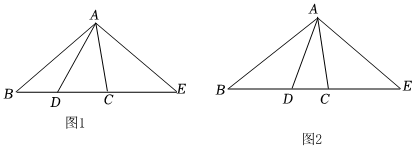
（1）如图1，若∠ADE=60°，∠CAE=40°，求∠BAD的度数；
（2）如图2，已知∠DAE=∠ADE．
①判断AD是否平分∠BAC，并说明理由；
②F为射线AD上一点（不与点D重合），过点F作FG⊥BC，垂足为G．若∠B=α，∠ACB=β，直接用含α，β的式子表示出∠AFG的度数．组卷：124引用：2难度：0.5 -
26．如图1，OP是∠MON的平分线，要求利用该图形画一对以OP所在直线为对称轴的全等三角形，方法如下：在∠MON的两边上用圆规截取长度相等的两条线段OB，OC，在角平分线上任取一点D，连接BD，CD，则△OBD≌△OCD，且它们关于OP所在直线对称．
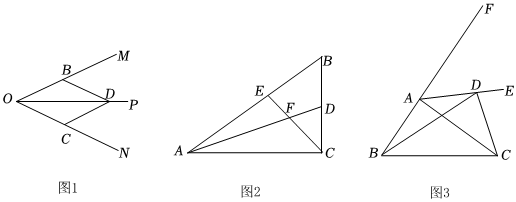
请你参考这个作全等三角形的方法，解答下列问题．
（1）如图2，在△ABC中，∠ACB是直角，∠B=60°，AD，CE分别是∠BAC和∠ACB的平分线，AD，CE相交于点F．
①∠EFA的度数为 ．
②请判断FE与FD的数量关系，并说明理由；
（2）如图3，AE是△ABC的外角∠FAC的平分线，D是射线AE上的一个动点（不与点A重合），猜想AB+AC与BD+DC的大小关系，并证明你的猜想．组卷：169引用：2难度：0.2
