2022-2023学年广东省梅州市丰顺县大同中学九年级（上）月考数学试卷（11月份）

一、选择题（共10题，共30分）

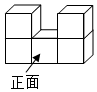• 1．如图，由5个完全相同的小正方体组合成一个立体图形，它的左视图为（　　）

  A．

  B．

  C．

  D．
  组卷：455引用：5难度：0.7

  解析

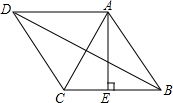• 2．如图，菱形ABCD的周长为8cm,高AE长为

  3

  cm,则对角线AC长和BD长之比为（　　）

  A．1：2

  B．1：3

  C．1： 2

  D．1： 3
  组卷：5981引用：79难度：0.9

  解析

• 3．在双曲线y=

  1

  -

  k

  x

  的任一分支上，y都随x的增大而增大，则下列说法错误的是（　　）

  A．k的值有可能为2

  B．图象位于第二、四象限

  C．若图象过点（a,b），也必过点（-a,-b）

  D．图象与x轴只有一个交点
  组卷：387引用：2难度：0.8

  解析

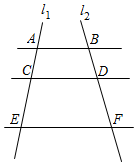• 4．如图，已知AB∥CD∥EF，它们依次交直线l₁、l₂于点A、C、E和点B、D、F．如果AC：CE=2：3，BD=4，那么BF等于（　　）

  A．6

  B．8

  C．10

  D．12
  组卷：216引用：3难度：0.7

  解析

• 5．某药品经过两次降价，每瓶零售价由168元降为128元．已知两次降价的百分率相同，每次降价的百分率为x,根据题意列方程得（　　）

  A．168（1+x）2=128	B．168（1-x）2=128
  C．168（1-2x）=128	D．168（1-x2）=128
  组卷：925引用：128难度：0.9

  解析

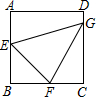• 6．如图，在正方形ABCD中，点E，F，G分别是AB，BC，CD上的点，EB=3，GC=4，∠FEG=60°，∠EGF=45°，则BC的长为（　　）

  A．3+ 4 3 3

  B． 7 3 3

  C．4+ 3

  D．3+4 3
  组卷：1351引用：3难度：0.7

  解析

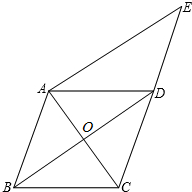• 7．如图，四边形ABCD是菱形，过点A作BD的平行线交CD的延长线于点E，则下列式子不成立的是（　　）

  A．DA=DE

  B．BD=CE

  C．∠EAC=90°

  D．∠ABC=2∠E
  组卷：461引用：52难度：0.9

  解析

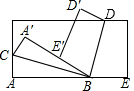• 8．将一张长方形纸片按如图所示的方式折叠，BC，BD为折痕，则∠CBD的度数为（　　）

  A．60°

  B．75°

  C．90°

  D．95°
  组卷：1472引用：132难度：0.9

  解析

三、解答题（共8小题，满分62分）

• 24．如图①，在正方形ABCD中，点E为BC边上任意一点（点E不与B、C重合），点F在线段AE上，过点F的直线MN⊥AE，分别交AB、CD于点M、N．
  （1）求证：MN=AE；
  （2）如图②，当点F为AE中点时，其他条件不变，连接正方形的对角线BD、MN与BD交于点G，连接BF．求证：BF=FG；
  （3）如图③，当点E为CB延长线上的动点时，如果（2）中的其他条件不变，直线MN分别交直线AB、CD于点M、N．结论“BF=FG”还成立吗？如果成立，请证明：如果不成立，请说明理由．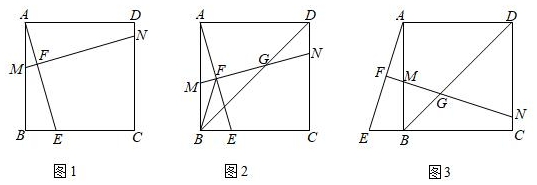
  
  组卷：707引用：7难度：0.1

  解析

• 25．有两张完全重合的矩形纸片，小亮同学将其中一张绕点A顺时针旋转90°后得到矩形AMEF（如图1），连接BD、MF，若此时他测得BD=8cm,∠ADB=30度．
  （1）试探究线段BD与线段MF的关系，并简要说明理由；
  （2）小红同学用剪刀将△BCD与△MEF剪去，与小亮同学继续探究．他们将△ABD绕点A顺时针旋转得△AB₁D₁，AD₁交FM于点K（如图2），设旋转角为β（0°＜β＜90°），当△AFK为等腰三角形时，请直接写出旋转角β的度数；
  （3）若将△AFM沿AB方向平移得到△A₂F₂M₂（如图3），F₂M₂与AD交于点P，A₂M₂与BD交于点N，当NP∥AB时，求平移的距离是多少？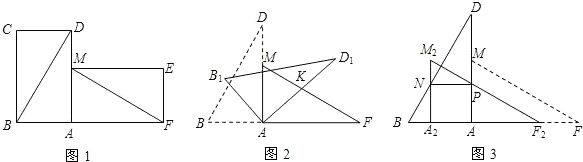
  
  组卷：1629引用：42难度：0.1

  解析