当前位置：试卷中心 > 试卷详情

2023-2024学年广东省深圳市宝安第一外国语学校高三（上）月考数学试卷（8月份）

发布：2024/8/18 3:0:1

1．设集合A={0，-a}，B={1，a-2，2a-2}，若A⊆B，则a=（　　）
A．2 B．1 C．
2
3
D．-1
组卷：5799引用：45难度：0.7
解析
2．若z=1+i,则|iz+3
z
|=（　　）
A．4
5
B．4
2
C．2
5
D．2
2
组卷：2848引用：7难度：0.7
解析
3．已知非零向量
a
，
b
，
c
，则“
a
•
c
=
b
•
c
”是“
a
=
b
”的（　　）
A．充分不必要条件 B．必要不充分条件
C．充分必要条件 D．既不充分也不必要条件
组卷：3634引用：38难度：0.8
解析
4．如图，
cos
（
θ
+
3
π
4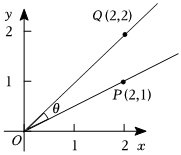
）
=（　　）
A．
-
2
5
5
B．
-
5
5
C．
-
4
5
D．
2
5
5
组卷：267引用：3难度：0.7
解析
5．若不等式x²-（a+1）x+a≤0的解集是[-4，3]的子集，则a的取值范围是（　　）
A．[-4，1] B．[-4，3] C．[1，3] D．[-1，3]
组卷：174引用：7难度：0.8
解析
6．向量|
a
|=|
b
|=1，|
c
|=
2
，且
a
+
b
+
c
=
0
，则cos〈
a
-
c
，
b
-
c
〉=（　　）
A．
-
1
5
B．
-
2
5
C．
2
5
D．
4
5
组卷：4035引用：4难度：0.8
解析

18．在锐角三角形△ABC中，角A，B，C的对边分别为a,b,c,
CD
为
CA
在
CB
方向上的投影向量，且满足
2
csin
B
=
5
|
CD
|
．
（1）求cosC的值；
（2）若
b
=
3
，a=3ccosB，求△ABC的周长．
组卷：968引用：13难度：0.6
解析
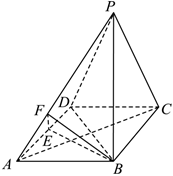19．如图，已知四棱锥P-ABCD的底面ABCD是菱形，平面PBC⊥平面ABCD，∠ACD=30°，E为AD的中点，点F在PA上，AP=3AF．
（1）证明：PC∥平面BEF；
（2）若∠PDC=∠PDB，且PD与平面ABCD所成的角为45°，求平面AEF与平面BEF夹角的余弦值．
组卷：584引用：9难度：0.5
解析

A．充分不必要条件	B．必要不充分条件
C．充分必要条件	D．既不充分也不必要条件

1．设集合A={0，-a}，B={1，a-2，2a-2}，若A⊆B，则a=（ ）