2022-2023学年安徽省安庆市怀宁县九年级（上）第三次月考数学试卷

一、选择题（本大题共10小题，每小题4分，满分40分）

• 1．若

  y

  x

  =

  3

  4

  ，则

  x

  +

  y

  x

  的值为（　　）

  A．1

  B． 4 7

  C． 5 4

  D． 7 4
  组卷：14055引用：164难度：0.9

  解析

• 2．在Rt△ABC中，∠C=90°，sinA=

  5

  13

  ，则cosB的值为（　　）

  A． 13 5

  B． 12 13

  C． 5 13

  D． 5 12
  组卷：457引用：4难度：0.7

  解析

• 3．抛物线y=-2x²-8x-9的顶点坐标是（　　）

  A．（2，1）

  B．（-2，1）

  C．（2，-1）

  D．（-2，-1）
  组卷：16引用：4难度：0.6

  解析

• 4．如图，点A为∠α边上的任意一点，作AC⊥BC于点C，CD⊥AB于点D，下列用线段比表示出sinα的值，正确的是（　　）

  A． BD BC

  B． AD AC

  C． AD DC

  D． CD AC
  组卷：26引用：4难度：0.6

  解析

• 5．已知α是锐角，2cos（α+45°）=1，则α的值是（　　）

  A．15°

  B．30°

  C．45°

  D．60°
  组卷：70引用：3难度：0.8

  解析

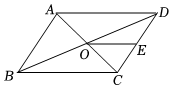• 6．如图，平行四边形ABCD中，对角线AC、BD相交于点O，点E是CD的中点，则△ODE与△ABC的面积比为（　　）

  A．1：2

  B．1：3

  C．1：4

  D．1：5
  组卷：69引用：3难度：0.5

  解析

• 7．若函数y=（a-1）x²-4x+2a的图象与x轴有且只有一个交点，则a的值为（　　）

  A．-1

  B．2

  C．-1或2

  D．-1或2或1
  组卷：2285引用：12难度：0.6

  解析

三、解答题（本大题共9小题，满分90分）

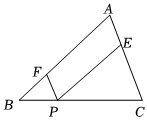• 22．为了在校园内有效开展劳动教育，东方红学校利用学校东南边靠墙的一块面积为单位1的Rt△ABC的空地，把这块空地划分成七八九年级三个部分，如图，在Rt△ABC中，点P是BC边上任意一点（点P与点B，C不重合），矩形AFPE的顶点F，E分别在AB，AC上．七年级为矩形AFPE部分，八九年级为△PEC和△BPF两部分．
  （1）若BP：PC=2：3，求S_△BPF；
  （2）已知BC=2，S_△ABC=1．设BP=x,矩形AFPE的面积为y,求y与x的函数关系式．
  （3）在（2）的情形下，考虑实际情况，要求七年级所分面积最大．求出七年级所分矩形AFPE部分的面积在x为多少时取得最大值，并求出最大值是多少．
  组卷：114引用：4难度：0.7

  解析

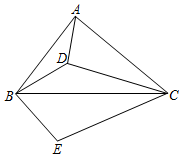• 23．如图，设D为锐角△ABC内一点，∠ADB=∠ACB+90°，过点B作BE⊥BD，BE=BD，连接EC．
  （1）求∠CAD+∠CBD的度数；
  （2）若AC•BD=AD•BC，
  ①求证：△ACD∽△BCE；
  ②求

  AB

  •

  CD

  AC

  •

  BD

  的值．
  组卷：1222引用：4难度：0.4

  解析