2022-2023学年北京市大兴区亦庄实验中学高一（下）期末数学试卷

一、选择题共10小题，每小题4分，共40分.在每小题列出的四个选项中，选出符合题目要求的一项.

• 1．已知复数z=-i（2+i），则z的共轭复数为（　　）

  A．1-2i

  B．2-i

  C．1+2i

  D．-1-2i
  组卷：156引用：4难度：0.8

  解析

• 2．设△ABC的内角A，B，C所对的边分别为a,b,c,若a=

  3

  ，b=1，A=60°，则B等于（　　）

  A．30°

  B．45°

  C．60°

  D．150°
  组卷：352引用：3难度：0.7

  解析

• 3．若圆柱的轴截面是一个正方形，其面积为4S，则它的一个底面面积是 （　　）

  A．4S

  B．4πS

  C．πS

  D．2πS
  组卷：424引用：3难度：0.9

  解析

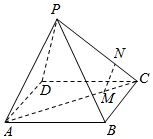• 4．如图，四棱锥P-ABCD中，M，N分别为AC，PC上的点，且MN∥平面PAD，则（　　）

  A．MN∥PD	B．MN∥PA
  C．MN∥AD	D．以上均有可能
  组卷：5980引用：29难度：0.9

  解析

• 5．在下列四个正方体中，A、B为正方体的两个顶点，M、N、Q为所在棱的中点，则在这四个正方体中，直线AB与平面MNQ不平行的是（　　）

  A．

  B．

  C．

  D．
  组卷：879引用：40难度：0.6

  解析

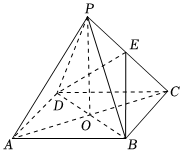• 6．阅读下面题目及其证明过程，在横线处应填写的正确结论是（　　）
  如图，四棱锥P-ABCD中，底面ABCD是正方形，O是正方形ABCD的中心，PO⊥底面ABCD，E是PC的中点，求证：平面PAC⊥平面BDE．
  证明：因为PO⊥底面ABCD，
  所以PO⊥BD．
  又因为AC⊥BD，且AC∩PO=O，
  所以__________．
  又因为BD⊂平面BDE，
  所以平面PAC⊥平面BDE．

  A．BD⊥平面PBC

  B．AC⊥平面PBD

  C．BD⊥平面PAC

  D．AC⊥平面BDE
  组卷：439引用：3难度：0.7

  解析

• 7．在△ABC中，若ac=8，a+c=7，

  B

  =

  π

  3

  ，则b=（　　）

  A．25

  B．5

  C．4

  D． 5
  组卷：1162引用：11难度：0.8

  解析

三、解答题共6小题，共85分.解答应写出文字说明，演算步骤或证明过程.

• 20．在△ABC中，a+b=11，再从条件①、条件②这两个条件中选择一个作为已知，求：
  （Ⅰ）a的值；
  （Ⅱ）sinC和△ABC的面积．
  条件①：c=7，cosA=-

  1

  7

  ；
  条件②：cosA=

  1

  8

  ，cosB=

  9

  16

  ．
  注：如果选择条件①和条件②分别解答，按第一个解答计分．
  组卷：5574引用：20难度：0.6

  解析

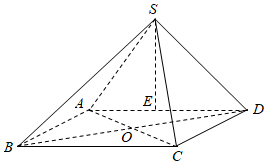• 21．如图，在四棱锥S-ABCD中，底面ABCD是边长为2的菱形，∠ABC=60°，SAD为正三角形．侧面SAD⊥底面ABCD，E、F分别为棱AD、SB的中点．
  （Ⅰ）求证：AF∥平面SEC
  （Ⅱ）求证：平面ASB⊥平面CSB
  （Ⅲ）在棱SB上是否存在一点M，使得BD⊥平面MAC？若存在，求

  BM

  BS

  的值；若不存在，请说明理由．
  组卷：931引用：6难度：0.3

  解析