2022-2023学年北京市东城区八年级（下）期末数学试卷
发布：2024/6/9 8:0:9
一、选择题。（本题共16分，每小题2分）第1-8题均有四个选项，符合题意的选项只有一个.
-
1．下列四个式子中，最简二次根式为（ ）
组卷：215引用：6难度：0.7 -
2．在平行四边形ABCD中，∠A：∠B：∠C：∠D的值可以是（ ）
组卷：1954引用：33难度：0.9 -
3．下列各式中，计算结果正确的是（ ）
组卷：213引用：3难度：0.7 -
4．奥运会的跳水项目是优美的水上运动，中国跳水队被称为“梦之队”，在一次女子单人10米台跳水比赛中，甲、乙两名选手五轮得分的折线统计图如图所示．设甲、乙的平均分依次为
，x甲，方差依次为S甲2，S乙2．以下四个推断中，正确的是（ ）x乙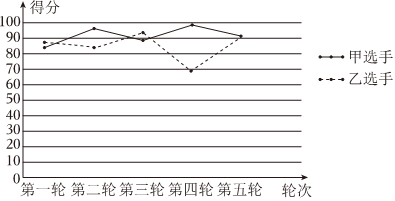
组卷：155引用：7难度：0.6 -
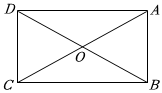5．如图，矩形ABCD的两条对角线相交于点O．若∠ACB=30°，AB=2，则边AD的长为（ ）组卷：296引用：4难度：0.7 -
6．在平面直角坐标系xOy中，点P（x1，y1），Q（x2，y2） 都在函数y=-2x+3的图象上，若x1＜x2＜0，则下列四个推断中错误的是（ ）
组卷：416引用：3难度：0.5 -
7．在平面直角坐标系xOy中，已知点A（-2，1），B（1，1）．若直线y=mx与线段AB有交点，则m的值不可能是（ ）
组卷：401引用：1难度：0.5 -
8．画一个四边形，使得该四边形的面积等于已知图形面积的一半．
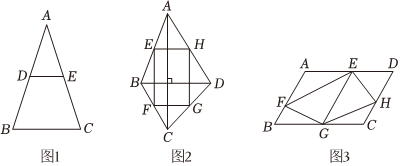
（1）如图1，已知等腰△ABC，D，E分别是AB，AC的中点，画四边形DBCE；
（2）如图2，已知四边形ABCD，AC⊥BD．四边的中点分别为E，F，G，H，画四边形EFGH；
（3）如图3，已知平行四边形ABCD，点E，G分别在AD，BC上，且EG∥AB，点F，H分别在AB，CD上，画四边形EFGH．
以上三种画法中，所有正确画法的序号是（ ）
组卷：344引用：3难度：0.5
二、填空题。（本题共16分，每小题2分）
-
9．若二次根式
有意义，则x的取值范围是 ．x-1组卷：4445引用：241难度：0.7
三、解答题。（本题共68分，第17题8分，第18-20题，每小题8分，第21题6分，第22-26题，每小题8分，第27-28题，每小题8分）解答应写出文字说明、演算步骤或证明过程。
-
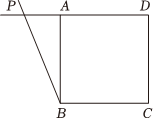27．如图，正方形ABCD．过点B作射线BP，交DA的延长线于点P．点A关于直线BP的对称点为E，连接BE，AE，CE．其中AE，CE分别与射线BP交于点G，H．
（1）依题意补全图形；
（2）设∠ABP=α，∠AEB=（用含α的式子表示），∠AEC=°；
（3）若EH=BH，用等式表示线段AE与CE之间的数量关系，并证明．组卷：870引用：2难度：0.5 -
28．在平面直角坐标系xOy中，对于线段MN和点P作出如下定义：若点M，N分别是线段PP1，PP2的中点，连接P1P2，我们称线段P1P2的中点Q是点P关于线段MN的“关联点”．
（1）已知点M（2，2），点P关于线段OM的“关联点”是点Q；
①若点P的坐标是（2，0），则点Q的坐标是 ；
②若点E的坐标是（1，-1），点F的坐标是（3，-1）．点P是线段EF上任意一点，求线段PQ长的取值范围；
（2）点A是直线l：y=x+1上的动点．在矩形ABCD中，边AB∥x轴，AB=3，BC=2．点P是矩形ABCD边上的动点，点P关于其所在边的对边的“关联点”是点Q．过点A作x轴的垂线，垂足为点G．设点G的坐标是（t,0）．当点A沿着直线l运动到点A′时，点G沿着x轴运动到点G'（t+m,0），点Q覆盖的区域的面积S满足20≤S≤30，直接写出m的取值范围．
组卷：730引用：2难度：0.2
